Solving quadratic equations and inequalities: Quadratic inequalities
 Solving quadratic inequalities via reduction and/or factorisation
Solving quadratic inequalities via reduction and/or factorisation
The steps in solving a quadratic inequality with one unknown via reduction are the same as in solving a quadratic equation by reduction:
- addition or subtraction of the same term on both sides;
- multiplication or division by the same nonzero number on both sides;
- Combination of similar terms.
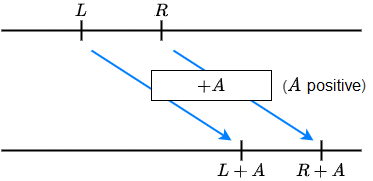
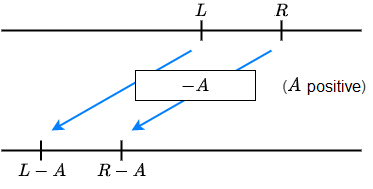
\(L<R\) is equivalent to
\(L+A<R+A\) and \(L-A<R-A\)
\(L>R\) is equivalent to
\(L+A>R+A\) and \(L-A>R-A\)
Here, \(A\) is an arbitrary expression.
Example
\[\begin{aligned} 4x^2+1&>5\\[0.25cm] 4x^2+1-1&>5-1\\[0.25cm] 4x^2&>4\end{aligned}\]
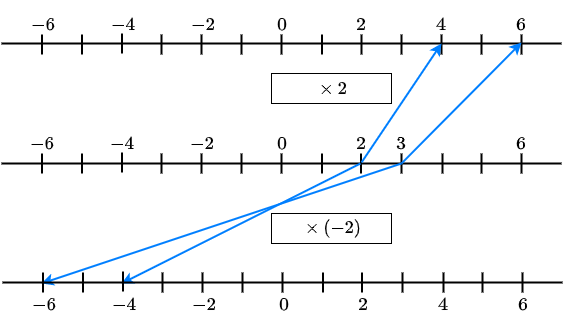
If \(A>0\), then \(L<R\) is equivalent to
\(A\cdot L<A\cdot R\) and \(\dfrac{L}{A}<\dfrac{R}{A}\)
If \(A>0\), then \(L>R\) is equivalent to
\(A\cdot L>A\cdot R\) and \(\dfrac{L}{A}>\dfrac{R}{A}\)
If \(A<0\), then \(L<R\) is equivalent to
\(A\cdot L>A\cdot R\) and \(\dfrac{L}{A}>\dfrac{R}{A}\)
If \(A<0\), then \(L>R\) equivalent is to
\(A\cdot L<A\cdot R\) and \(\dfrac{L}{A}<\dfrac{R}{A}\)
Here, \(A\) is an arbitrary nonzero number.
Examples
\[\begin{aligned} -x^2&< 1\\[0.25cm] (-1)\cdot (-x^2)&\gt(-1)\cdot 1\\[0.25cm] x^2&\gt -1\\[0.75cm]-2x^2&>8\\[0.25cm]\dfrac{-2x^2}{-2}&<\dfrac{8}{-2}\\[0.25cm] x^2&<4\end{aligned}\]
With the above rules, you can solve quadratic inequalities, i.e., reduce to an inequality in which the unknown is isolated and on the left-hand side of a inequality. Completing the square and factorisation by inspection are often productive strategies.
Solving quadratic inequalities by completing the square Suppose that reduction and completing the square has led to the inequality \[a(x+p)^2+q<0\] for certain real numbers \(a\), \(p\), \(q\) with\(a\neq 0\).
If \(a>0\), then this is equivalent to the inequality \((x+p)^2<\dfrac{q}{a}\). We distinguish three cases:
- if \(q<0\), then there are no solutions.
- as \(q=0\), then \(x=-p\) is the only solution.
- as \(q>0\), then \(-\sqrt{\dfrac{q}{a}}<x+p<\sqrt{\dfrac{q}{a}}\), that is \(-p-\sqrt{\dfrac{q}{a}}<x<-p+\sqrt{\dfrac{q}{a}}\)
If \(a<0\) then this is equivalent to the inequality \((x+p)^2>\dfrac{q}{a}\). We distinguish three cases:
- if \(q<0\) then all real numbers satisfy the inequalite because a square of a real number is always greater than or equal to \(0\).
- as \(q=0\), then \(x=-p\) the only solution.
- as \(q>0\), then \(x+p<-\sqrt{\dfrac{q}{a}}\;\vee x+p>\sqrt{\dfrac{q}{a}}\), that is \(x<-p-\sqrt{\dfrac{q}{a}}\;\vee\;x<-p+\sqrt{\dfrac{q}{a}}\)
Solving a quadratic inequality via factorisation by inspection Suppose that you can write the inequality as \[a(x+p)(x+q)>0\] for certain real numbers \(a\), \(p\), \(q\) with \(a\neq 0\).
If \(a>0\), then this is equivalent to the inequality \((x+p)(x+q)>0\). We distinguish two cases:
- if \(x+p>0\) and \(x+q>0\), then \(x>-p\) and \(x>-q\), that is \(x>\max(-p,-q)\).
- if \(x+p<0\) and \(x+q<0\), then \(x<-p\) and \(x<-q\), that is \(x<\min(-p,-q)\).
If \(a<0\), then the inequality is equivalent to \((x+p)(x+q)<0\) with solution \(\min(-p,-q)<x<\max(-p,-q)\).
Illustrative examples: