Calculating with letters: Computing with letters
The banana method for expanding double brackets
The banana method
For the product of two two-terms, we have the banana method:
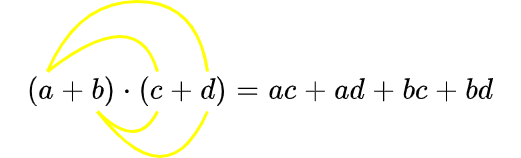
Examples
\[\begin{aligned} (a+2)(b+3) &=a\cdot b+a\cdot 3+2\cdot b + 2\cdot 3\\ &= ab+3a+2b+6\\[0.3cm] (-4a+2)(2b-1) &= -4a\cdot 2b+-4a\cdot -1\\ &\phantom{=\,\,} +2\cdot 2b+2\cdot -1\\ &=-8ab+4a+4b-2\end{aligned}\]
Area model A third method for illustrating the banana method is the area model with rectangles. For example, the formula \((n+2)(n+1)=n^2+3n+1\) can be visualised with rectangles in the following way:
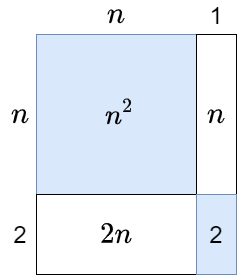
With the banana method you can expand the double pairs of brackets. A square of a two-term can be seen here as the product of two identical two-terms. The formula can also be used in all kinds of complicated situations. Sometimes you can collect terms after expansion of brackets with the banana formula.
\[\begin{aligned}(10c-3)(-5c+10) &= (10c)\cdot (-5c)+(10c)\cdot 10+(-3)\cdot (-5c)+(-3)\cdot 10\\
&\phantom{abcdevwxyz}\blue{\text{the banana method}}\\ &= -50c^2+100c+15c-30\\
&\phantom{abcdevwxyz}\blue{\text{simplification of terms}}\\ &=-50c^2+ 115c-30\\
&\phantom{abcdevwxyz}\blue{\text{collection of similar terms}}\end{aligned}\]
