Multiple integrals: Double integrals
Double integrals approximated with a Riemann sum
Approximate the double integral \[\iint_R 4\,x\,y\,\dd(x,y)\] with \[R=[0,1]\times[0,1]\] via a Riemann sum over evenly divided partition with mesh size\(\frac{1}{2}\). That is, we divide the square \(R\) into four sub-squares with sides of length \(\frac{1}{2}\) and we index them as shown in the figure below.
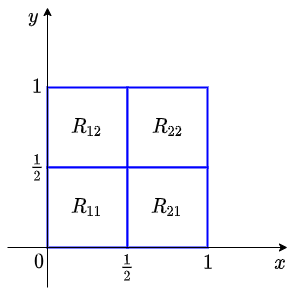
Within each sub-square \(R_{ij}\) we take the hoekpunt linksonder as tag \(s_{ij}\). Use this to calculate the Riemann sum and compare it to the exact result which is equal to \(1\).
Do the same, but now choose the hoekpunt linksboven as tag \(s_{ij}\) of the subs-square \(R_{ij}\)
| \(\iint_R 4\,x\,y\,\dd(x,y)\approx{}\) | with hoekpunt linksonder as tag. |
| \(\iint_R 4\,x\,y\,\dd(x,y)\approx{}\) | with hoekpunt linksboven as tag. |
Unlock full access
