Meervoudige integralen: Dubbelintegralen
Dubbelintegralen benaderd met een Riemann-som
Benader de dubbelintegraal
met
via een Riemann-som over een regelmatige verdeling met maaswijdte . Dat willen zeggen dat we het vierkant verdelen in vier deelvierkantjes met zijden van lengte en indexeren ze zoals in onderstaande figuur te zien is.
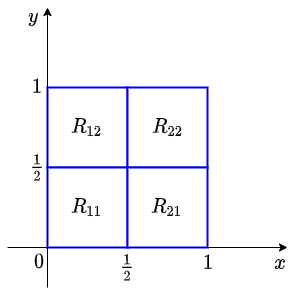
Binnen elk deelvierkantje nemen we als strooipunt het hoekpunt linksboven. Gebruik dit om de Riemann-som te berekenen en vergelijk het met het exacte resultaat dat gelijk is aan .
Doe hetzelfde, maar kies nu het hoekpunt linksonder als strooipunt van het deelvierkantje
| met hoekpunt linksboven als strooipunt. |
| met hoekpunt linksonder als strooipunt. |
Ontgrendel volledige toegang
