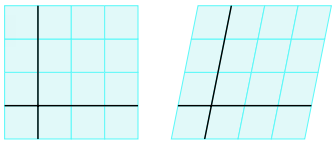
Vectors: The notion of vector and vector space
Coordinate system
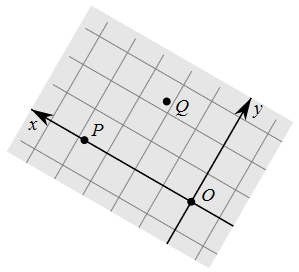
Skew coordinate system To create a coordinate system in a plane we need three points, say \(O\), \(Q_1\) and \(Q_2\), that are not aligned. We choose the point \(O\) as the origin in the plane. We can use the line \(OQ_1\) as the first coordinate axis and the line \(OQ_2\) as the second coordinate axis. We can then give the points \(Q_1\) and \(Q_2\) the coordinates \((1,0)\) and \((0,1)\), respetively. Each point \(P\) in the plane can then be written as the addition of two vectors along the coordinate axes, which are multiples of the vectors \(\vec{OQ_1}\) and \(\vec{OQ_2}\). The scalars are the coordinates of the point \(P\). The vectors \(\vec{OQ_1}\) and \(\vec{OQ_2}\) are called unit vectors in the coordinate system of the plane. See the figure below with a skew coordinate system .
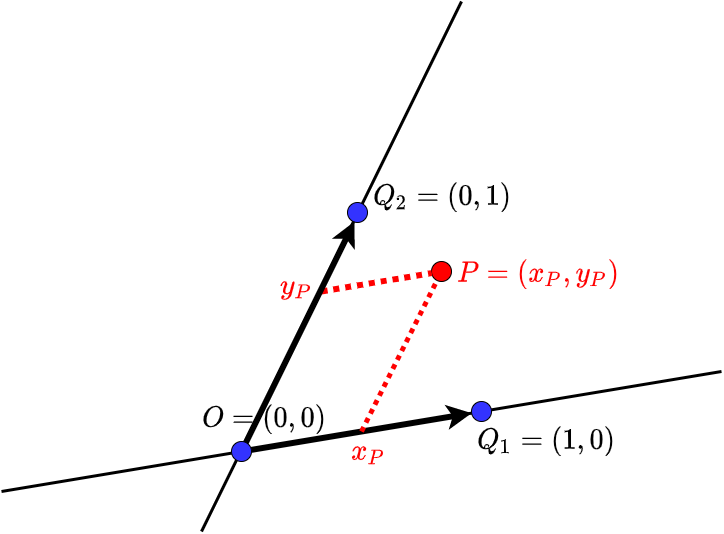The coordinate axes in this coordinate system can be regarded as number lines and each number on a coordinate axis corresponds to a point on the axis and thus to a vector from the origin along the coordinate axis.
Cartesian coordinate system In a Cartesian coordinate system, the coordinate axes are mutually perpendicular to each other and the concept of length along both axes is chosen to be the same. In the figure below, the two unit vectors are drawn in blue and red. The points in the plane with integer coordinates together form a grid. In the figure below the grid lines are also drawn so that you get graph paper (the turquoise colouring is only there for decoration).
Skewed graph paper A grid for a coordinate system is not exclusively defined for a Cartesian coordinate system. The figure below illustrates how skew graph paper can also be made with a skew coordinate system. Grid points in this coordinate system again have integer coordinates and the grid lines are parallel to one of the two coordinate axes.
Construction of a Cartesian coordinate system for three points We can define a Cartesian coordinate system in the plane of our choice. We can do this for any three points, say \(O\), \(P\) and \(Q\), that are not lying on a single line in such a way that
- the point \(O\) has coordinates \((0,0)\),
- the point \(P\) has coordinates \((p,0)\) for some \(p>0\),
- the point \(Q\) has coordinates \((q_1, q_2)\) for some \(q_1 \) and \(q_2\) with \(q_2 > 0\).
See the figure below.
Apart from scaling, this Cartesian coordinate system is unique. Such a construction of a Cartesian coordinate system helps to translate geometric problems into problems that can be described in coordinates and can be solved with them.
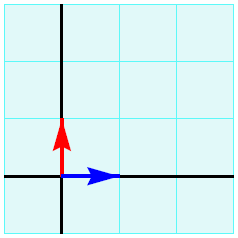
With a choice of a Cartesian coordinate system in a plane, we get a coordinate plane that we denote \(\mathbb{R}^2\). Similarly, we can construct a coordinate system in a three-dimensional space from four points that are not lying in a single plane. If the coordinate axes are mutually perpendicular and have the same scaling, we again speak of a Cartesian coordinate system and there is a coordinate space that we denote \(\mathbb{R}^3\)
