Optelling, scalaire vermenigvuldiging en lineaire combinatie Je kunt vectoren optellen, met een scalar vermenigvuldigen en combineren. Dit gaat op de manier die je zou mogen verwachten. Het enige opmerkelijke aan optelling, maar wat wel een prettige bijkomstigheid blijkt te zijn, is dat je ook een getal bij een vector mag optellen of aftrekken en dat dit dan als een vector van geschikte lengte met alleen maar dat gegeven getal wordt opgevat zodat de optelling betekenis heeft.

> u <- 1:2; v<- 3:4
> u + v
[1] 4 6
> 5*u
[1] 5 10
> 5*u - 2*v
[1] -1 2
> u + 1
[1] 2 3

Vermenigvuldiging, inproduct, uitproduct en Hadamard product Tot nu toe zijn we het inproduct, het uitproduct en het Hadamard product tegengekomen. Python faciliteert deze berekeningen:

>> u <- 1:3; v <- 4:6 
> sum(u*v)  # standaard inproduct van vectoren
[1] 32      
> library(pracma); dot(u,v) # alternatief via pracma packge
[1] 32
> u %*% v          # alternatief via matrixvermenigvuldiging
    [,1]
[1,]  32
> cross(u,v)       # uitproduct via pracma package
[1] -3 6 -3 
array([-3, 6, -3]) 
> u*v              # Hadamard product
[1] 4 10 18>> u * v           

Rekenkundige bewerkingen Met het vermenigvuldigingsteken * geef je aan dat je vermenigvuldiging componentsgewijs wilt toepassen. Dit kan je ook met andere rekenkundige operatoren doen zoals deling en machtsverheffing. Op deze manier kun je ook snel vectoren construeren die gedefinieerd zijn door indexeringsfuncties of eenvoudig grafieken van functies maken. We geven wat voorbeelden ter illustratie

> u <- 3:4; v <- 5:6
> u / v
[1] 0.6000000 0.6666667
> u * u
[1] 9 16
> u * u
[1] 9 16
> sqrt(sum(u^2))   # berekening van de Euclidische lengte van u
[1] 5 
> i <- 1:5; v <- 1/(i+1); v # v_i = 1/(i+1)
[1] 0.5000000 0.3333333 0.2500000 0.2000000 0.1666667
> t <- seq(0, pi, 0.01)
> s <- sin(t)
> p <- t - 1/6*t^3 + 1/120*t^5 - 1/5040*t^7;
> # grafiek van sinus (in blauw) en veeltermfunctie p (in rood)
> plot(t, s, type="l", col="blue", lwd=2)
> lines(t, p, type="l", col="red", lwd=2)

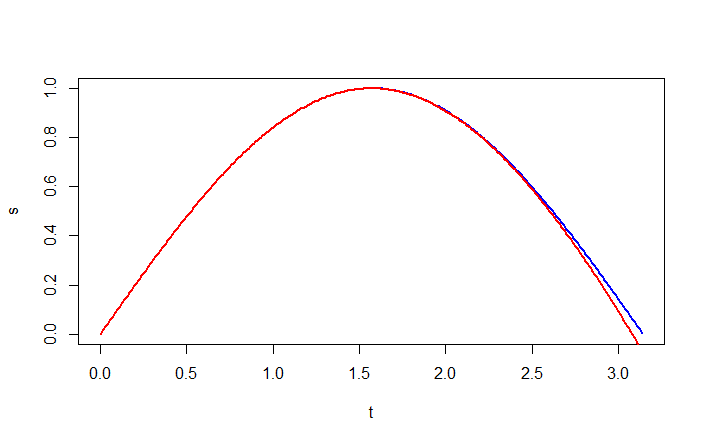
Vectorisatie Het laatste voorbeeld van een sinusgrafiek illustreert ook dat R 'begrijpt' dat de enige zinvolle toepassing van wiskundige functies op vectoren is dat ze componentsgewijs gebruikt worden. Deze manier van werken heet vectorisatie en maakt de R taal zo bondig en helder. We geven nog een paar voorbeelden ter illustratie.

> x <- 1:5; x
[1] 1 2 3 4 5
> options(digits=4)  # format voor decimale getallen
> sqrt(x)
[1] 1.000 1.414 1.732 2.000 2.236
> log(x)
[1] 0.0000 0.6931 1.0986 1.3863 1.6094
> exp(x)
[1] 2.718 7.389 20.086 54.598 148.413
> i <- 1:6; v <- (-1)^i/i; v # v_i=(-1)^i/i
[1] -1.0000 0.5000 -0.3333 0.2500 -0.2000 0.1667
> minmax <- c(min(v), max(v));  minmax  # minimum en maximum
[1] -1.0 0.5
> sum(v)     # sommatie van alle componenten
[1] -0.6167
> cumsum(v)  # cummulatieve sommatie
[1] -1.0000 -0.5000 -0.8333 -0.5833 -0.7833 -0.6167
> sv <- sign(v);  sv  # tekens van de componenten
[1] -1 1 -1 1 -1 1
> dsv <- diff(sv); dsv  # verschillen in opeenvolgende tekens
[1] 2 -2 2 -2 2 
> i <- (1:length(dsv))[dsv>0]; i  # indices met overging van - naar + teken in v
[1] 1 3 5