Algebra with vectors in a plane

Vectors: The notion of vector and vector space

Algebra with vectors in a plane

Equality Two vectors \(\vec{u}\) and \(\vec{v}\) in a geometric plane are equal to each other, \(\vec{u}=\vec{v}\), if they have the same length and direction.

Opposite The opposite of a vector \(\vec{v}\) is defined as the vector with the same length but having the opposite direction. We denote the opposite of vector \(\vec{v}\) as \(-\vec{v}\).

Scalar multiplication The product of a number \(\lambda\) with a vector \(\vec{v}\) is defined as the vector obtained from\(\vec{v}\) by scaling it relative to its initial point with a scale factor \(|\lambda|\), provided that we first reverse the direction of the vector \(\vec{v}\) if \(\lambda \lt 0\). We write this product as \(\lambda \cdot\vec{v}\).

So, \(\lambda \cdot\vec{v}\) is the vector whose

length is \(\left|\lambda\right|\) times the length of \(\vec{v}\) , and
direction is equal to that of \(\vec{v}\) if \(\lambda\gt 0\) and equal to that of \(-\vec{v}\) if \(\lambda \lt 0\).

We call \(\lambda \cdot\vec{v}\) a scalar multiple of \(\vec{v}\) or simply a multiple of \(\vec{v}\). The (scaling) number \(\lambda\) with which we scale the vector is called a scalar. Usually we write

\(\vec{v}\) instead of \(1\cdot\vec{v}\);
\(-\vec{v}\) instead of \((-1)\cdot\vec{v}\);
\(2\,\vec{v}\) instead of \(2\cdot\vec{v}\), and so on;
\(-2\cdot \vec{v}\) and \(-2\,\vec{v}\) instead of \((-2)\cdot\vec{v}\), and so on.

All scalar multiples of a vector \(\vec{v}\) form together the span of \(\vec{v}\), denoted as \(\langle\vec{v}\rangle\).

Greek letters Scalars are often denoted by Greek letters, but this is not obligatory: For example, \(k\cdot \vec{v}\) is the scalar multiple of the vector \(\vec{v}\) with the number \(k\).

Scalar equal to zero If \(\lambda=0\), then the direction of the scalar multiple \(\lambda \cdot\vec{v}\) is indeterminate and \(\lambda \cdot\vec{v}=\vec{0}\).

Below is an interactive figure that illustrates how scalar multiplication of a vector \(\vec{v}\) works. For reasons of clarity, we have drawn a blue colour representative of the scalar multiple \(\lambda\cdot\vec{v}\) that does not go through the origin. With the slider you can modify the scalar \(\lambda\).

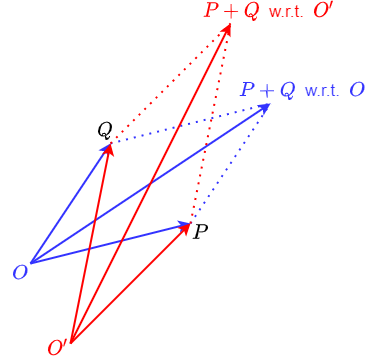
Sum and difference of vectors Two position vectors can be added and the result is again a position vector, namely the one obtained through the construction of a parallelogram:

Move \(\vec{u}\) and/or \(\vec{v}\) to observe how the sum of two position vectors can be determined.

The sum of two vectors \(\vec{u}\) and \(\vec{v}\) can also be obtained by laying \(\vec{u}\) and \(\vec{v}\) head-to-tail, as shown in the figure below:

Move \(\vec{u}\) and/or \(\vec{v}\) to see how adding vectors goes in this way. If one of the two vectors is a scalar multiple of the other, you can only use the second construction.

What remains is the definition of the sum of the zero vector with a vector \(\vec{v}\) as \(\vec{v}+\vec{0}=\vec{0}+\vec{v}=\vec{v}\).

Instead of \(\vec{u}+(-\vec{v})\) we usually write \(\vec{u}-\vec{v}\). This expression is called the difference of \(\vec{u}\) and \(\vec{v}\); we subtract \(\vec{v}\) from \(\vec{u}\).

Dependence of vector addition on the choice of the origin Addition (and subtraction) of equivalence classes of free vectors in a plain is determined by the head-to-tail method. This does not depend on the pair o points that one can choose as representatives for a vector. This is different for vector addition in a coordinate plane. In the coordinate plane belong to each point in the plane a position vector as soon as we fix the origin of the coordinate system. Then we can define addition (and subtraction) via a parallelogram construction. Then the result depends on the choice of the origin; have a look at what happens in the figure below at a different choice of the origin (\(\O'\)).

vector addition