Vectoren: De begrippen vector en vectorruimte
Algebra met vectoren in een vlak
Gelijkheid Twee vectoren \(\vec{u}\) en \(\vec{v}\) in een meetkundig vlak zijn gelijk aan elkaar, \(\vec{u}=\vec{v}\), als ze dezelfde lengte en richting hebben.
Tegengestelde De tegengestelde van een vector \(\vec{v}\) is gedefinieerd als de vector met dezelfde lengte maar met tegengestelde richting. We noteren de tegengestelde van vector \(\vec{v}\) als \(-\vec{v}\).
Scalaire vermenigvuldiging Het product van een getal \(\lambda\) met een vector \(\vec{v}\) wordt gedefinieerd als de vector die uit \(\vec{v}\) ontstaat door deze vanuit zijn beginpunt met een getal \(|\lambda|\) te schalen, met dien verstande dat we de richting van de vector \(\vec{v}\) eerst omkeren als \(\lambda \lt 0\). We noteren dit product als \(\lambda \cdot\vec{v}\).
Dus: \(\lambda \cdot\vec{v}\) is de vector waarvan
- de lengte \(\left|\lambda\right|\) maal de lengte van \(\vec{v}\) is en
- de richting gelijk aan die van \(\vec{v}\) is als \(\lambda\gt 0\) en gelijk aan die van \(-\vec{v}\) is als \(\lambda \lt 0\).
We noemen \(\lambda \cdot\vec{v}\) een scalair veelvoud van \(\vec{v}\) of kortweg veelvoud van \(\vec{v}\). Het (schalings)getal \(\lambda\) waarmee we de vector vermenigvuldigen noemen we een scalar (meervoud: scalairen). Doorgaans schrijven we
- \(\vec{v}\) in plaats van \(1\cdot\vec{v}\);
- \(-\vec{v}\) in plaats van \((-1)\cdot\vec{v}\);
- \(2\,\vec{v}\) in plaats van \(2\cdot\vec{v}\), enzovoort;
- \(-2\cdot \vec{v}\) en \(-2\,\vec{v}\) in plaats van \((-2)\cdot\vec{v}\), enzovoort.
Alle scalaire veelvouden van een vector \(\vec{v}\) vormen samen de drager van \(\vec{v}\), ook wel het opspansel van \(\vec{v}\) genoemd en genoteerd als \(\langle\vec{v}\rangle\).
Hieronder staat een interactieve figuur die illustreert hoe scalaire vermenigvuldiging van een vector \(\vec{v}\) werkt. De blauw gekleurde vector hoort bij het scalaire veelvoud \(\lambda\cdot\vec{v}\).
Wijzig met de schuifbalk de scalar \(\lambda\) en bekijk het effect.
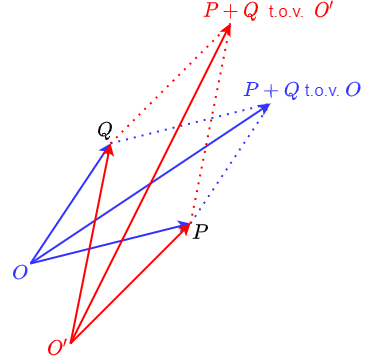
Som en verschil van vectoren Twee plaatsvectoren kun je bij elkaar optellen en het resultaat is weer een plaatsvector, die verkregen wordt via de constructie van een parallellogram:
Verplaats \(\vec{u}\) en/of \(\vec{v}\) om te zien hoe de som van twee plaatsvectoren bepaald kan worden.
De som van twee vectoren \(\vec{u}\) en \(\vec{v}\) is ook te bepalen door \(\vec{u}\) en \(\vec{v}\) kop aan staart te leggen, zoals aangegeven in onderstaande figuur:
Verplaats \(\vec{u}\) en/of \(\vec{v}\) om te zien hoe optellen van plaatsvectoren op deze manier gaat. Als een van beide vectoren een scalair veelvoud is van de ander, dan kun je enkel de tweede constructie gebruiken.
Rest ons nog de optelling met de nulvector met een vector \(\vec{v}\) te definiëren als \(\vec{v}+\vec{0}=\vec{0}+\vec{v}=\vec{v}\).
In plaats van \(\vec{u}+(-\vec{v})\) schrijven we doorgaans \(\vec{u}-\vec{v}\). Deze uitdrukking wordt het verschil van \(\vec{u}\) en \(\vec{v}\) genoemd.
Afhankelijkheid van vectoroptelling van de keuze van de oorsprong Optelling (en verschil) van equivalentieklassen van vrije vectoren in een vlak is met de kop-staart-methode vastgelegd. Dit hangt dan niet af van de puntenparen die men kan kiezen als representanten voor de vector. Dat is anders bij een vectoroptelling in een coördinaatvlak. In het vlak hoort bij elk punt een unieke plaatsvector zodra we een oorsprong vastleggen. We kunnen dan de optelling en het verschil definiëren via een parallellogramconstructie. Maar dan hangt het resultaat wel af van de keuze van de oorsprong; zie maar in onderstaande figuur wat er gebeurt bij een keuze van een andere oorsprong (\(\O'\)).
