Vectors in ℝ² and ℝ³

Vectors: The notion of vector and vector space

Vectors in ℝ² and ℝ³

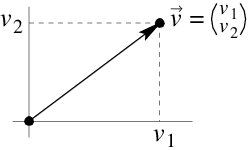
Once you choose a coordinate system in a geometric plane or space, you can describe a position vector with the coordinates of its terminal point. A position vector \(\vec{v}\) in a coordinate plane with terminal point \((v_1,v_2)\) is often denoted by \( \begin{pmatrix} v_1 \\ v_2\end {pmatrix}\). The individual coordinates \(v_1\) and \(v_2\) are called the components of the vector \(\vec{v}\).

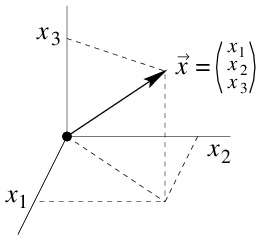
Similarly, a point \(P=(p_1,p_2,p_3)\) in the three-dimensional coordinate space \(\mathbb{R}^3\) is the terminal point of a position vector \(\vec{p} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end {pmatrix} \).

We used above the column notation for vectors. This notation is much more popular than the row notation for vectors.

Convention Unless otherwise stated, we use the column notation for vectors, that is, we write vectors with the components below each other.

The coordinate plane \(\mathbb{R}^2=\{(x,y)\mid x,y\in\mathbb{R}\}\) consists of points and not of vectors. But if you identify a position vector in a plane with its terminal point, then the subtle difference between point and vector disappears. Therefore, we may also write \[\mathbb{R}^2=\left\{ \begin{pmatrix} x \\ y\end{pmatrix} \middle|\, x\in\mathbb{R},y\in\mathbb{R}\right\}\qquad\text{and}\qquad \mathbb{R}^3=\left\{\begin{pmatrix} x \\ y\\ z \end{pmatrix}\middle|\, x\in\mathbb{R},y\in\mathbb{R},z\in\mathbb{R}\right\}\tiny.\]

Calculus with vectors in a plane or space Scalar multiplication and addition of vectors in \(\mathbb{R}^2\) and \(\mathbb{R}^3\) goes componentwise.

Dimension 2

If \(\lambda\in\mathbb{R}\), \(\vec{u} = \begin{pmatrix} u_1 \\ u_2\end {pmatrix} \) and \(\vec{v} = \begin{pmatrix} v_1 \\ v_2\end {pmatrix} \), then \[\begin{aligned}\lambda\cdot \vec{v} &= \lambda\cdot \begin{pmatrix} v_1 \\ v_2\end{pmatrix}=\begin{pmatrix} \lambda\cdot v_1 \\ \lambda\cdot v_2\end{pmatrix} \\ \\ \vec{u}+\vec{v} &= \begin{pmatrix} u_1\\ u_2\end{pmatrix} + \begin{pmatrix} v_1 \\ v_2\end{pmatrix} = \begin{pmatrix} u_1+v_1 \\ u_2+v_2\end{pmatrix}\end{aligned}\]

Dimension 3

If \(\lambda\in\mathbb{R}\), \(\vec {u} = \begin{pmatrix} u_1 \\ u_2\\ u_3\end {pmatrix} \), and \(\vec {v} = \begin{pmatrix} v_1 \\ v_2\\ v_3\end {pmatrix} \), then \[\begin{aligned}\lambda\cdot \vec{v} &= \begin{pmatrix} \lambda\cdot v_1 \\ \lambda\cdot v_2 \\ \lambda\cdot v_3 \end{pmatrix} \\ \\ \vec{u}+\vec{v} &= \begin{pmatrix} u_1+v_1 \\ u_2+v_2\\ u_3+v_3\end{pmatrix}\end{aligned}\]