Vectoren in ℝ² en ℝ³

Vectoren: De begrippen vector en vectorruimte

Vectoren in ℝ² en ℝ³

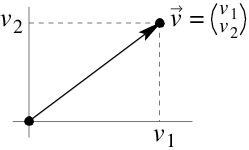
Zodra je een assenstelsel in een meetkundig vlak of ruimte kiest, dan kun je een plaatsvector beschrijven met de coördinaten van zijn eindpunt. Een plaatsvector \(\vec{v}\) in een coördinatenvlak met eindpunt \((v_1,v_2)\) noteren we vaak als \(\begin{pmatrix} v_1 \\ v_2\end{pmatrix}\). De individuele coördinaten \(v_1\) en \(v_2\) worden de componenten van de vector \(\vec{v}\) genoemd.

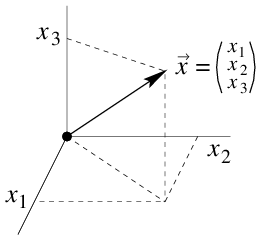
Evenzo is een punt \((x_1,x_2,x_3)\) in de driedimensionale coördinatenruimte \(\mathbb{R}^3\) het eindpunt van een plaatsvector \(\vec{x} =\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}\).

We hebben hierboven de kolomnotatie voor vectoren gebruikt. In boeken kun je ook de rijnotatie voor vectoren tegenkomen, maar de kolomnotatie is het meest gangbaar.

Afspraak Tenzij anders vermeld, gebruiken we de kolomnotatie voor vectoren, dat wil zeggen, schrijven we vectoren met de componenten onder elkaar.

Het coördinaatvlak \(\mathbb{R}^2=\{(x,y)\mid x,y\in\mathbb{R}\}\) bestaat uit punten en niet uit vectoren. Maar als je een plaatsvector in een vlak identificeert met zijn eindpunt, dan verdwijnt het subtiele verschil tussen punt en vector. Daarom mogen we ook wel schrijven\[\mathbb{R}^2=\left\{ \begin{pmatrix} x \\ y\end{pmatrix} \middle|\, x\in\mathbb{R},y\in\mathbb{R}\right\}\qquad\text{en}\qquad \mathbb{R}^3=\left\{\begin{pmatrix} x \\ y\\ z \end{pmatrix}\middle|\, x\in\mathbb{R},y\in\mathbb{R},z\in\mathbb{R}\right\}\tiny.\]

Rekenen met vectoren in vlak en ruimte Scalaire vermenigvuldiging en optelling van vectoren in \(\mathbb{R}^2\) en \(\mathbb{R}^3\) gaat componentsgewijs.

2-dimensionaal

Als \(\lambda\in\mathbb{R}\), \(\vec{u}=\begin{pmatrix} u_1 \\ u_2\end{pmatrix}\) en \(\vec{v}=\begin{pmatrix} v_1 \\ v_2\end{pmatrix}\), dan \[\begin{aligned}\lambda\cdot \vec{v} &= \lambda\cdot \begin{pmatrix} v_1 \\ v_2\end{pmatrix}=\begin{pmatrix} \lambda\cdot v_1 \\ \lambda\cdot v_2\end{pmatrix} \\ \\ \vec{u}+\vec{v} &= \begin{pmatrix} u_1\\ u_2\end{pmatrix} + \begin{pmatrix} v_1 \\ v_2\end{pmatrix} = \begin{pmatrix} u_1+v_1 \\ u_2+v_2\end{pmatrix}\end{aligned}\]

3-dimensionaal

Als \(\lambda\in\mathbb{R}\), \(\vec{u}=\begin{pmatrix} u_1 \\ u_2\\ u_3\end{pmatrix}\) en \(\vec{v}=\begin{pmatrix} v_1 \\ v_2\\ v_3\end{pmatrix}\), dan \[\begin{aligned}\lambda\cdot \vec{v} &= \begin{pmatrix} \lambda\cdot v_1 \\ \lambda\cdot v_2 \\ \lambda\cdot v_3 \end{pmatrix} \\ \\ \vec{u}+\vec{v} &= \begin{pmatrix} u_1+v_1 \\ u_2+v_2\\ u_3+v_3\end{pmatrix}\end{aligned}\]