Vectors: The notion of vector and vector space
 The n-dimensional coordinate space
The n-dimensional coordinate space
The 2-dimensional coordinate plane \(\mathbb{R}^2\) and the 3-dimensional coordinate space \(\mathbb{R}^3\) can be generalized.
The n-dimensional coordinate space For each natural number \(n\) we define the space \(\mathbb{R}^n\) as the set of ordered \(n\)-tuples denoted either by row or column vectors: \[\mathbb{R}^n = \left\{{\small\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}}\; \middle|\; x_1, x_2,\ldots, x_n\in\mathbb{R}\right\}\]
We define for this set a componentewise addition and a scalar multiplication so that it becomes a vector space: \[{\small\lambda\cdot \begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}} = {\small\begin{pmatrix}\lambda\cdot x_1\\ \lambda\cdot x_2\\ \vdots\\ \lambda\cdot x_n\end{pmatrix}}\qquad(\text{with }\lambda\in\mathbb{R})\] and \[ {\small\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}} + {\small\begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix}} = {\small\begin{pmatrix}x_1+y_1\\x_2+y_2\\\vdots\\x_n+y_n\end{pmatrix}}\]
A vector \(\vec{x}\) in \(\mathbb{R}^n\) has \(n\) components, which we usually call coordinates and simply denote as \(x_1, x_2,\ldots,x_n\). The zero vector in \(\mathbb{R}^n \) is a column vector that only consists of zeros. Formally you should write the zero vector \(\vec{0}\) write, but for convenience we often denote it simply as \(0\), too.
Unit Vectors The following vectors \[ \vec{e_1} = {\small \begin{pmatrix}1\\0\\0\\ \vdots\\0\end{pmatrix}},\quad \vec{e_2} = {\small \begin{pmatrix}0\\1\\0\\ \vdots\\0\end{pmatrix}}, \ldots,\quad
\vec{e_{n-1}} = {\small \begin{pmatrix}0\\ \vdots\\0\\ 1\\0\end{pmatrix}},\quad \vec{e_n} = {\small \begin{pmatrix}0\\ \vdots\\0\\ 0\\1\end{pmatrix}}\] are called the unit vectors of \(\mathbb{R}^n\). The unit vectors span the space \(\mathbb{R}^n\). After all, \[\vec{x}=x_1\cdot \vec{e_1}+x_2\cdot \vec{e_2}+\cdots+x_n\cdot \vec{e_n}\] Because the unit vectors are linearly independent they form a basis of \(\mathbb{R}^n\).
\(\phantom{x}\)
We will encounter the \(n\)-dimensional coordinate space again and again, and not only as geometric plane or space. We gave a few examples
Neural activity The activity, for example the firing frequencies \(r_1,\ldots, r_n\), of \(n\) simultaneously sampled neurons can be described by an \(n\)-dimensional vector \(\vec{r} = {\small \begin{pmatrix}r_1\\ \vdots\\ r_n\end {pmatrix}} \).
Similarly you describe electrical activity recorded on \(n\) electrodes in an EEG measurement as an \(n\)-dimensional vector.
Colour The colour of a pixel, for example, the RGB colour, can be described by three values in a column vector \(\vec{c}={\small\cv{r\\ g\\ b}}\) .
Similarly, the absorption spectrum of conical light sensitive cells in the retina can be described according to the trichromatic theory of human colour perception by three values in a column vector \(\vec{v}={\small\cv{L\\ M\\ S}}\). The three values correspond with the three types of cones in the retina. The symbols \(L\), \(M\) and \(S\) represent the sensitivity of long, medium and short wavelength of light (in a loose relationship with the colours red, green, blue). Each colour triggers activity in all three kinds of cone systems, but a specific combination of activity levels defines the colour of the light shining in the eyes. Colour blindness can related to the lack of cones of a certain type, and in this case, the visibility is mathematically reduced to a two-dimensional space.
You could not tell at first glance, but the last example of sensitivity of cells in the retina is actually about vector spaces of functions. \(L\), \(M\) and \(S\) are functions of the wavelength of light and span a 3-dimensional vector space. The figure below shows the graphs of the normalized function in the visible light spectrum with wavelength between 400 and 700 nm.
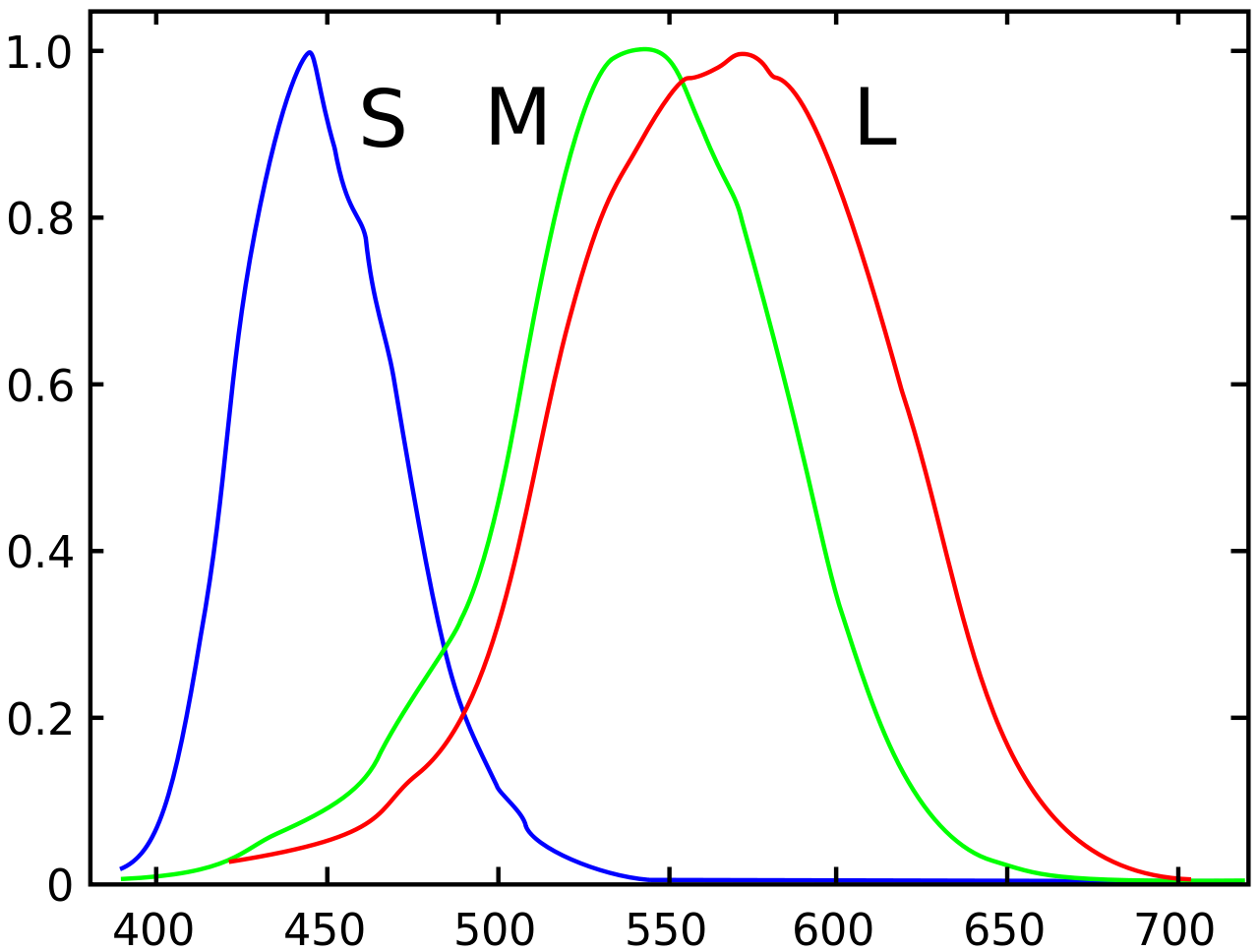
The linear combination \(L+M+
S\) corresponds, for instance, according to the theory of complementary colours and opponent processes of colour perception with the achromatic clarity or luminance of a light signal, i.e., the linear combination codes black versus white. The linear combination \(L+M-S\) codes yellow versus blue, and the lineair combination \(L-M+S\) codes red versus green.


