Vectoren: De begrippen vector en vectorruimte
 De n-dimensionale coördinaatruimte
De n-dimensionale coördinaatruimte
Het 2-dimensionale coördinaatvlak \(\mathbb{R}^2\) en de 3-dimensionale coördinaatruimte \(\mathbb{R}^3\) kunnen veralgemeniseerd worden.
De n-dimensionale coördinaatruimte Voor elk natuurlijk getal \(n\) definiëren we de ruimte \(\mathbb{R}^n\) als de verzameling van geordende \(n\)-tallen die we naar smaak als rij- of kolomvectoren noteren (wij kiezen in deze cursus altijd kolomnotatie): \[\mathbb{R}^n = \left\{{\small\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}}\; \middle|\; x_1, x_2,\ldots, x_n\in\mathbb{R}\right\}\]
We kunnen hierop een componentsgewijze optelling en scalaire vermenigvuldiging definiëren waardoor het een vectorruimte wordt: \[{\small\lambda\cdot \begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}} = {\small\begin{pmatrix}\lambda\cdot x_1\\ \lambda\cdot x_2\\ \vdots\\ \lambda\cdot x_n\end{pmatrix}}\qquad(\text{met }\lambda\in\mathbb{R})\] en \[ {\small\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}} + {\small\begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix}} = {\small\begin{pmatrix}x_1+y_1\\x_2+y_2\\\vdots\\x_n+y_n\end{pmatrix}}\]
Een vector \(\vec{x}\) in \(\mathbb{R}^n\) heeft \(n\) componenten, die we gewoonlijk coördinaten noemen en stilzwijgend noteren als \(x_1, x_2,\ldots,x_n\). De nulvector in \(\mathbb{R}^n\) is een kolomvector die alleen uit nullen bestaat. Formeel moet je voor de nulvector \(\vec{0}\) schrijven, maar gemakshalve noteren we dit vaak ook kortweg als \(0\).
Eenheidsvectoren De volgende vectoren \[ \vec{e_1} = {\small \begin{pmatrix}1\\0\\0\\ \vdots\\0\end{pmatrix}},\quad \vec{e_2} = {\small \begin{pmatrix}0\\1\\0\\ \vdots\\0\end{pmatrix}}, \ldots,\quad
\vec{e_{n-1}} = {\small \begin{pmatrix}0\\ \vdots\\0\\ 1\\0\end{pmatrix}},\quad \vec{e_n} = {\small \begin{pmatrix}0\\ \vdots\\0\\ 0\\1\end{pmatrix}}\] heten de eenheidsvectoren van \(\mathbb{R}^n\). De eenheidsvectoren spannen de ruimte \(\mathbb{R}^n\) op. Immers \[\vec{x}=x_1\cdot \vec{e_1}+x_2\cdot \vec{e_2}+\cdots+x_n\cdot \vec{e_n}\] Omdat de eenheidsvectoren ook lineair onafhankelijk zijn vormen ze een basis van \(\mathbb{R}^n\).
\(\phantom{x}\)
De \(n\)-dimensionale coördinaatruimte zullen we keer op keer tegenkomen, en niet alleen als meetkundig vlak of ruimte. We gegeven enkele voorbeelden.
Neurale activiteit De activiteit, bijvoorbeeld de vuurfrequenties \(r_1,\ldots, r_n\), van \(n\) simultaan bemonsterde neuronen kan beschreven worden als een \(n\)-dimensionale vector \(\vec{r}= {\small\begin{pmatrix}r_1\\ \vdots\\ r_n\end{pmatrix}}\).
Evenzo kun je de elektrische activiteit op \(n\) elektroden bij een EEG-meting beschrijven als een \(n\)-dimensionale vector.
Kleur De kleur van een pixel, bijvoorbeeld de RGB-kleur, kan beschreven worden met drie waarden in een kolomvector \(\vec{c}={\small\cv{r\\ g\\ b}}\).
Evenzo kan de absorptiespectrum door kegelvormige lichtgevoelige cellen in de retina volgens de trichromatische theorie van kleurwaarneming beschreven worden met drie waarden in een kolomvector \(\vec{v}={\small\cv{L\\ M\\ S}}\). De drie waarden horen bij de drie typen kegeltjes in de retina. De letters \(L\), \(M\) en \(S\) staan voor gevoeligheid van de kegelvormige cellen voor lange, middellange en korte golflengtes van licht (losjes in verband staand met de kleuren rood, groen en blauw). Elke kleur lokt volgens de trichromatische theorie voor kleurwaarneming activiteit uit in alle drie soorten van kegeltjesystemen, maar specifieke combinatie van activiteitsniveaus definieert de kleur van het licht dat in de ogen schijnt, of beter gezegd de perceptie van een tint. Kleurenblindheid kan te maken hebben met het ontbreken van kegeltjes van een zeker type en in dit geval is het zicht wiskundig teruggebracht tot een twee-dimensionale ruimte.
Je zou het op het eerste gezicht niet zeggen, maar het laatste voorbeeld van lichtgevoeligheid van cellen in de retina gaat eigenlijk over vectorruimtes van functies: \(L\), \(M\) en \(S\) zijn functies van de golflengte van licht en spannen een 3-dimensionale vectorruimte op. Onderstaande figuur toont de grafieken van de genormaliseerde functies in het zichtbare spectrum van golflengtes tussen 400 en 700 nm.
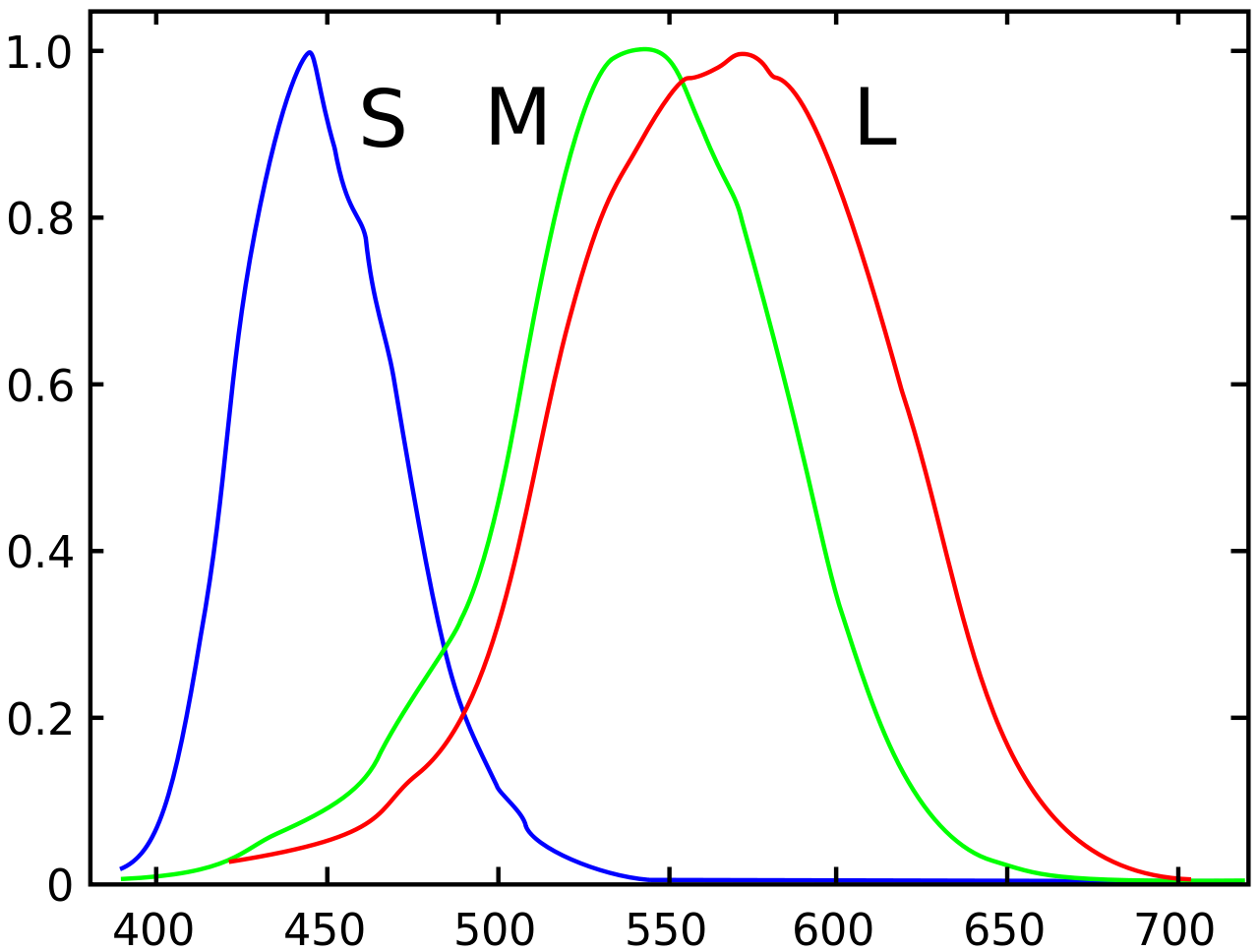
De lineaire combinatie \(L+M+S\) correspondeert bijvoorbeeld volgens de theorie van complementaire kleuren en opponente processen voor kleurwaarneming met de achromatische helderheid of luminantie van een lichtsignaal, anders gezegd codeert de lineaire combinatie zwart versus wit. De lineaire combinatie \(L+M-S\) codeert voor geel versus blauw en de lineaire combinatie \(L-M+S\) codeert voor groen versus rood.


