Vectors: Lines and planes
Vector representation of a line and plane in ℝ³
Also lines in the three-dimensional space can be described via vector representations. We re just need a support vector and a direction vector.
Vector representation of a line The vectors \(\vec{x}\) that point to the points on a straight line \(\ell\) can be generally described by a so-called vector representation (or parametric representation), that is, with a recipe of the following form: \[\ell : \,\vec{x} = \vec{u} + \lambda\cdot\vec{v}\] Here, the scalar \(\lambda\), also called in this context parameter, can be freely chosen and the only restrictions on the vectors \(\vec{u}\) and \(\vec{v}\) is that they are 3-dimensional and that \(\vec{v}\) is not the zero vector.
More interesting is that we can represent planes in the three-dimension space in a similar manner.
Vector representation of a plane The vectors \(\vec{x}\) that point to the points on a plane \(\mathcal{V}\) can be generally described by a so-called vector representation (or parametric representation), that is, with a recipe of the following form: \[\mathcal{V} : \,\vec{x} = \vec{u} + \lambda\cdot\vec{v}+ \mu\cdot\vec{v}\] Here, the scalars \(\lambda\) and \(\mu\), also called in this context parameters, can be freely chosen and the only restrictions on the vectors \(\vec{u}\), \(\vec{v}\), and \(\vec{w}\) are that they are 3-dimensional and that \(\vec{v}\) and \(\vec{w}\) not a multiple of each other.
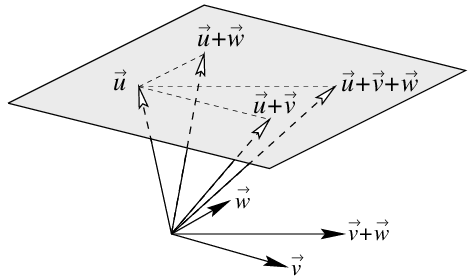
The vector \(\vec{u}\) is a support vector of the plane \(\mathcal{V}\); it points to a certain point on the plane. The vectors \(\vec{v}\) and \(\vec{w}\) are called direction vectors.
Instead of \(\lambda\) and \(\mu\) you may skip mathematical convention and use other letters. Henceforth we will also use \(r\) and \(s\) in excercises because it is easier to enter them in SOWISO than Greek letters. In that case, pay attention to your handwriting because otherwise you may have difficulty in distinguishing for instance the letter \(s\) and the digit \(5\) (which would result in mistakes).
The geometry of a vector representation of a plane can be visualized as follows:
Look at the following examples to learn how to determine
- a vector representation of a plane when the equation is known;
- an equation of a plane, in the form \(a\cdot x+b\cdot y+c\cdot z=d\), for a given vector representation of the plane;
- a vector representation of a plane through three points that do not lie on one line.
(There are more correct answers.)
Substitute \( y =\lambda \) and \(z=\mu\) in the given equation. We can express \( x\) in terms of \(\lambda\) and \(\mu\) as follows: \[\begin{aligned}
x-5\,\lambda-3\,\mu &= -6\\ & \phantom{abcxyz} \blue{\text{substitution of }y=\lambda\text{ and }z=\mu}\\[0.1cm]
x &= 5\,\lambda+3\,\mu-6 \\ & \phantom{abcxyz} \blue{\text{isolation of } x}\end{aligned}\]
The vectors with terminal points on the plane \(\mathcal{V}\) therefore can be written as \[\begin{aligned}
\cv{x\\y\\z} &= \cv{-6+\lambda\cdot 5 +\mu\cdot 3\\ \lambda\\ \mu}\\ \\
&=\cv{-6\\0\\0}+\lambda \cdot\cv{5\\1\\ 0}+\mu\cdot \cv{3\\0\\ 1}\tiny.
\end{aligned}\]
More correct vector representations are possible: For example, any vector with terminal point on the plane can be used as a support vector and also other direction vectors can be computed as linear combinations of the calculated direction vectors.
Plücker coordinates of a line Another description of lines in the threedimensional space is possible and used in computer vision. Click on Advanced to look at the bonus for math enthusiasts.
