Vectoren: Rechte lijnen en vlakken
Vectorvoorstelling van een lijn en vlak in ℝ3
Ook lijnen in de 3-dimensionale ruimte kunnen we beschrijven met behulp van vectorvoorstellingen. We hebben opnieuw enkel een steunvector en een richtingsvector nodig.
Vectorvoorstelling van een lijn De vectoren \(\vec{x}\) die de punten op een rechte lijn \(\ell\) aanwijzen laten zich in het algemeen beschrijven met een zogenaamde vectorvoorstelling (of parametervoorstelling), d.w.z. met een recept van de volgende vorm: \[\ell : \,\vec{x} = \vec{u} + \lambda\cdot\vec{v}\] Hierin is de scalar \(\lambda\), ook wel in deze context parameter genoemd, vrij te kiezen en is de enige restrictie op de vectoren \(\vec{u}\) en \(\vec{v}\) dat ze 3-dimensionaal zijn en dat \(\vec{v}\) niet de nulvector is.
Interessanter is dat we op een soortgelijke manier platte vlakken in de ruimte kunnen representeren.
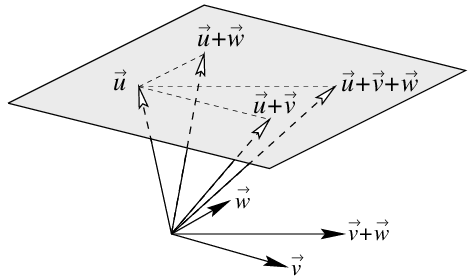
Vectorvoorstelling van een vlak De vectoren \(\vec{x}\) die de punten op een plat vlak \(\mathcal{V}\) aanwijzen laten zich in het algemeen beschrijven met een zogenaamde vectorvoorstelling (of parametervoorstelling), d.w.z. met een recept van de volgende vorm: \[\mathcal{V} : \,\vec{x} = \vec{u} + \lambda\cdot\vec{v}+ \mu\cdot\vec{w}\] Hierin zijn de scalairen \(\lambda\) en \(\mu\), ook wel in deze context parameters genoemd, vrij te kiezen en is de enige restrictie op de vectoren \(\vec{u}\), \(\vec{v}\) en \(\vec{w}\) dat ze 3-dimensionaal zijn en dat \(\vec{v}\) en \(\vec{w}\) geen veelvoud van elkaar zijn.
De vector \(\vec{u}\) is een steunvector van het vlak \(\mathcal{V}\); deze wijst naar een zeker punt op het vlak. De vectoren \(\vec{v}\) en \(\vec{w}\) heten richtingsvectoren.
In plaats van \(\lambda\) en \(\mu\) mag je afwijken van wiskundige conventies en andere letters gebruiken. Wij zullen in opgaven ook \(r\) en \(s\) gebruiken omdat ze gemakkelijker in te toetsen zijn in SOWISO dan de Griekse letters. Maar let er op dat je dan op papier netjes schrijft, want anders kan je bijvoorbeeld de letter \(s\) en het cijfer \(5\) misschien niet goed onderscheiden van elkaar (waardoor je dan fouten maakt).
Meetkundig ziet zo'n vectorvoorstelling er als volgt uit:
Bekijk de volgende voorbeelden om te leren hoe
- een vectorvoorstelling te bepalen bij een gegeven vergelijking van een vlak;
- een vergelijking van een vlak, van de vorm \(a\cdot x+b\cdot y+c\cdot z=d\), te vinden bij een gegeven vectorvoorstelling;
- een vectorvoorstelling van een vlak door drie punten die niet op één lijn liggen te bepalen.
(er zijn meerdere correcte oplossingen)
Substitueer \( y =\lambda \) en \(z=\mu\) in de gegeven vergelijking. We kunnen nu \( x\) als volgt uitdrukken in \( \lambda\) en \(\mu\): \[\begin{aligned}
-2\,x+4\,\lambda-3\,\mu &= -9\\ & \phantom{abcxyz} \blue{\text{substitutie van }y=\lambda\text{ en }z=\mu}\\[0.1cm]
x &= {{4\,\lambda-3\,\mu+9}\over{2}} \\ & \phantom{abcxyz} \blue{\text{isolatie van } x}\\[0.1cm] x &={{9}\over{2}}+\lambda\cdot 2 +\mu\cdot -{{3}\over{2}} \\ & \phantom{abcxyz}\blue{\text{uitwerking}}\end{aligned}\]
De vectoren met eindpunten op het vlak \(\mathcal{V}\) zijn dus te schrijven als \[\begin{aligned}
\cv{x\\y\\z} &= \cv{{{9}\over{2}}+\lambda\cdot 2 +\mu\cdot -{{3}\over{2}}\\ \lambda\\ \mu}\\ \\
&=\cv{{{9}\over{2}}\\0\\0}+\lambda \cdot\cv{2\\1\\ 0}+\mu\cdot \cv{-{{3}\over{2}}\\0\\ 1}\tiny.
\end{aligned}\]
Er zijn meer correcte vectorvoorstellingen mogelijk: elke vector met eindpunt op het vlak kan bijvoorbeeld als steunvector gebruikt worden en ook kunnen andere richtingsvectoren berekend worden als lineaire combinatie van de zojuist berekende richtingsvectoren.
Plücker coördinaten van een lijn Een andere beschrijving van lijnen in de driedimensionale ruimte is mogelijk en wordt in het vakgebied computer vision gebruikt. Klik op Verdieping om de toegift voor de liefhebber te bekijken.
