Dot product, angle and orthogonal projection

Vectors: Distance, angle, dot product and cross product

Dot product, angle and orthogonal projection

Dot product in 2D and 3D

We define the scalar product or dot product of vectors \(\vec{u}=\cv{u_1\\ u_2}\) and \(\vec{v}=\cv{v_1\\ v_2}\) in the coordinate plane \(\mathbb{R}^2\) as \[\vec{u}\boldsymbol{\cdot}\vec{v}=u_1\cdot v_1+u_2\cdot v_2 \]

We define the scalar product or standard dot product of v \(\vec{u}=\cv{u_1\\ u_2\\ u_3}\) and \(\vec{v}=\cv{v_1\\ v_2\\v_3}\) in the coordinate plane \(\mathbb{R}^3\) we define as \[\vec{u}\boldsymbol{\cdot}\vec{v}=u_1\cdot v_1+u_2\cdot v_2+ u_3\cdot v_3\]

Examples

\[\begin{aligned}\cv{2\\3}\boldsymbol{\cdot}\cv{4\\5}&=2\cdot 4+3\cdot 5\\ &=8+15=23\\ \\ \cv{2\\3}\boldsymbol{\cdot}\cv{3\\-2}&=2\cdot 3+3\cdot -2\\ &=6-6=0\\ \\ \cv{2\\3\\4}\boldsymbol{\cdot}\cv{5\\6\\-7}&=2\cdot 5+3\cdot 6+4\cdot -7=0\end{aligned}\]

This can be generalized to the \(n\)-dimensional coordinate space \(\mathbb{R}^n\).

The scalar (dot) product The scalar product or dot product of two vectors \(\vec{u}=\cv{u_1\\ \vdots \\ u_n}\) and \(\vec{v}=\cv{v_1\\ \vdots \\ v_n}\) in the \(n\)-dimensional space \(\mathbb{R}^n\), also referred to as the standard inner product, is defined as \[\vec{u}\boldsymbol{\cdot}\vec{v}=u_1\cdot v_1+u_2\cdot v_2 +\cdots+ u_n\cdot v_n=\sum_{i=1}^n u_i\cdot v_i\]

We write standard inner product because, in the coordinate space, other inner products can be defined. For example, you can define in \(\mathbb{R}^2\) also the inner product \[\vec{u}\cdot \vec{v}=u_1v_1-u_1v_2-u_2v_1+3u_2v_2\] This definition then has similar properties as the standard inner product.

Note that for a vector \(\vec{v}\) in \(\mathbb{R}^n\) it we have \[\lVert v\rVert^2=\vec{v}\boldsymbol{\cdot} \vec{v}\]

Usually we just talk about the scalar product, dot product, or inner product if we mean the standard inner product and there is no possible confusion. The name dot product explains our choice of notation with a bold point. Other common formats that you may encounter in books and papers are \(\langle \vec{u},\vec{v}\rangle\) and \((\vec{u},\vec{v})\).

What is the exact value of the dot product of the vectors below?

\(\cv{8\\ 5} \boldsymbol{\cdot} \cv{3\\ 4}={}\)\( 44 \)

After all:\[\begin{aligned} \cv{8\\ 5}\boldsymbol{\cdot}\cv{3\\ 4} &= (8\cdot 3) + (5 \cdot 4) &\blue{\text{definition of dot product}} \\
&=44 &\blue{\text{final result}} \end{aligned}\]

New example

Properties of the dot product the dot product on \(\mathbb{R}^n\) has the following properties for all scalars \(\alpha\) and \(\beta\), and for all vectors \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) :

Symmetry: \(\vec{u}\boldsymbol{\cdot} \vec{v} = \vec{v}\boldsymbol{\cdot} \vec{u}\)
Linearity: \(\left(\alpha\,\vec{u}+\beta\,\vec{v}\right)\boldsymbol{\cdot} \vec{w} = \alpha\,\vec{u}\boldsymbol{\cdot} \vec{w}+\beta\,\vec{v}\boldsymbol{\cdot} \vec{w}\)
Standard: The inner product of a vector with itself is the square of the length, ie, \(\vec{v}\boldsymbol{\cdot} \vec{v}= \lVert\vec{v}\rVert^2\) for each vector \(\vec{v}\). The inner product is nonnegative and is equal to zero only if \(\vec{v}=\vec{0}\).

All properties can be proved in case of \(\mathbb{R}^2\), \(\mathbb{R}^3\) and \(\mathbb{R}^n\) by working out all expression in terms of coordinates and by applying the coordinatewise definitions of addition and scalar multiplication.

The properties mentioned above are exactly those that are needed for a vector space \(V\) to have an inner product \(\boldsymbol{\cdot} : V\times V\longrightarrow \mathbb{R}\) defined and become a so-called inner product space.

For example, the set of real continuous functions over the interval \([0,1]\) with the usual addition and scalar multiplication is a vector space in which we can define an inner product as \[f\boldsymbol{\cdot}g = \int_0^1 f(x)\cdot g(x)\,dx\]

Given the dot product \(\vec{u}\boldsymbol{\cdot} \vec{v}= 6\), what is then the exact value of the dot product \(\left(-2\vec{u}\right)\boldsymbol{\cdot}\left( 2\vec{v}\right)\,\)?

\(\left(-2\vec{u}\right)\boldsymbol{\cdot}\left( 2\vec{v}\right)={}\) \(-24\).

After all, using of the properties of the dot product we get \[\begin{aligned}\left(-2\vec{u}\right)\boldsymbol{\cdot}\left( 2\vec{v}\right) &= -2\cdot 2 \cdot \left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)\\ &=
-4\cdot\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)\\
&=-4\cdot 6\\
&=-24\\
\end{aligned}\]

New example

Geometric meaning of the dot product The dot product in the plane \(\mathbb{R}^2\) and in the space \(\mathbb{R}^3\) has the following geometrical meaning:

The inner product \(\vec{u}\boldsymbol{\cdot}\vec{v}\) of two vectors \(\vec{u}\) and \(\vec{v}\) is equal to the product of the length of \(\vec{u}\) and the length of the projection of \(\vec{v}\) on the span of \(\vec{u}\).

In other words, the orthogonal projection of vector \(\vec{v}\) on the span of vector \(\vec{u}\) is equal to \(\left(\frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\vec{u}\boldsymbol{\cdot}\vec{u}}\right)\vec{u}\).

With reference to the figure below, we have the following formula: \[\vec{u}\boldsymbol{\cdot}\vec{v} = \lVert\vec{u}\rVert\cdot\lVert\vec{v}\rVert\cdot\cos(\phi)\tiny.\]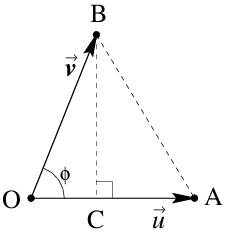

Using the above properties of the dot product we can compute \(\lVert\vec{u}-\vec{v}\rVert^2\) as follows: \[\begin{aligned}\lVert\vec{u}-\vec{v}\rVert^2 &= (\vec{u}-\vec{v})\boldsymbol{\cdot} (\vec{u}-\vec{v})\\ &= \vec{u}\boldsymbol{\cdot}\vec{u} - 2\,\vec{u}\boldsymbol{\cdot}\vec{v}+ \vec{v}\boldsymbol{\cdot}\vec{v}\\ &= \lVert\vec{u}\rVert^2+\lVert\vec{v}\rVert^2-2\,\vec{u}\boldsymbol{\cdot}\vec{v}\tiny.\end{aligned}\] We can also compute \(\lVert\vec{u}-\vec{v}\rVert^2\) directly. Let \(\phi\) be the (short) angle between the two vectors \(\vec{u}\) and \(\vec{v}\), where \(0\le \phi\le \pi\). The terminal points of the vectors \(\vec{u}\) and \(\vec{v}\) are called \(A\) and \(B\), respectively. From \(B\) we draw a line that is perpendicular to the span of \(\vec{u}\) and call the intersection point of these two lines \(C\).

Furthermore: \(\text{length of line segment }BC=\lVert\vec{v}\rVert\sin\phi\) and \(\text{length of line segment }OC=\lVert\vec{v}\rVert\cos\phi\). We can now compute \(\lVert\vec{u}-\vec{v}\rVert^2\) via the Pythagorean theorem: \[\begin{aligned} \lVert\vec{u}-\vec{v}\rVert^2 &= \lVert\vec{AB}\rVert^2=\lVert\vec{BC}\rVert^2+\lVert\vec{CA}\rVert^2= \lVert\vec{BC}\rVert^2+\left(\lVert\vec{OA}\rVert-\lVert\vec{OC}\rVert\right)^2\\ &= \lVert\vec{v}\rVert^2\sin^2\!\phi+\left(\lVert\vec{u}\rVert-\lVert\vec{v}\rVert\cos\phi\right)^2 \\ &= \lVert\vec{u}\rVert^2+ \lVert\vec{v}\rVert^2\left(\sin^2\!\phi+\cos^2\!\phi\right)-2\,\lVert\vec{u}\rVert\,\lVert\vec{v}\rVert\,\cos\phi \\ &= \lVert\vec{u}\rVert^2 + \lVert\vec{v}\rVert^2-2\,\lVert\vec{u}\rVert\,\lVert\vec{v}\rVert\,\cos\phi\end{aligned}\] Comparing the two expressions \(\lVert\vec{u}-\vec{v}\rVert^2\), we find \[\vec{u}\boldsymbol{\cdot}\vec{v} = \lVert\vec{u}\rVert\,\lVert\vec{v}\rVert\,\cos\phi\]

Conversely, we can define an angle between two vectors via the dot product (or more generally via an inner product).

Angle between two vectors The (short) angle \(\phi\) between two nonzero vectors \(\vec{u}\) and \(\vec{v}\) is defined by the formula \[\cos(\phi) = \frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\lVert\vec{u}\rVert\cdot\lVert\vec{v}\rVert}\qquad (\text{with }0\le \phi\le \pi)\] This angle is acute if \(\vec{u}\boldsymbol{\cdot}\vec{v}>0\), and obtuse if \(\vec{u}\boldsymbol{\cdot}\vec{v}<0\).

We also notice that \(\vec{u}\boldsymbol{\cdot}\vec{v}=0\) means exactly that the vectors \(\vec{u}\) and \(\vec{v}\) are perpendicular to each other. We also say that the vectors \(\vec{u}\) and \(\vec{v}\) are orthogonal.

The following inequality is now evident in the plane \(\mathbb{R}^2\) and the space \(\mathbb{R}^3\) . This inequality, and herewith the concept of angle, generalizes to \(\mathbb{R}^n\).

Cauchy-Schwarz inequality Let \(\vec{u}\) and \(\vec{v}\) be vectors in \(\mathbb{R}^n\) then \[\left|\vec{u}\boldsymbol{\cdot}\vec{v}\right|\le \lVert\vec{u}\rVert\cdot\lVert\vec{v}\rVert\]

In fact, the Cauchy-Schwarz inequality is true for any inner product spaces. In the proof we only need to apply properties of the inner product.

If \(\vec{v}=\vec{0}\), then the statement is correct. So we may assume that \(\vec{v}\neq\vec{0}\) and introduce the number \(\lambda=\frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\lVert\vec{v}\rVert^2}\). Then the following it true: \[\begin{aligned}0&\leq \lVert\vec{u}-\lambda\vec{v}\rVert^2 \\ \\ &= \left(\vec{u}-\lambda\vec{v}\right) \boldsymbol{\cdot}\left(\vec{u}-\lambda\vec{v}\right) \\ \\ &= \vec{u}\boldsymbol{\cdot}\vec{u} - 2\lambda\vec{u}\boldsymbol{\cdot}\vec{v}+\lambda^2\vec{v}\boldsymbol{\cdot}\vec{v} \\ \\ &= \lVert\vec{u}\rVert^2-\frac{\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)^2}{\lVert\vec{v}\rVert^2}\end{aligned}\] So \[ \frac{\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)^2}{\lVert\vec{v}\rVert^2}\le \lVert\vec{u}\rVert^2\] and thus \[\left|\vec{u}\boldsymbol{\cdot}\vec{v}\right|\le \lVert\vec{u}\rVert\cdot \lVert\vec{v}\rVert\tiny.\]

The vector \(\vec{u}\) has length \(7\) and the vector \(\vec{v}\) has length \(9\). The angle between the two vectors is equal to \(150^{\circ}\).

What is the exact value of the inner product \(\vec{u}\boldsymbol{\cdot} \vec{v}\,\)?

\(\vec{u}\boldsymbol{\cdot}\vec{v}={}\) \(-\frac{63}{2}\sqrt{3}\)

After all, if \(\phi\) is the angle between the vectors \(\vec{u}\) and \(\vec{v}\), then\[\begin{aligned}\vec{u}\boldsymbol{\cdot}\vec{v} &= \lVert\vec{u}\rVert\cdot\lvert\vec{v}\rvert\cdot \cos(\phi)\\ \\
&= 7 \cdot 9 \cdot\cos\left(150^{\circ}\right)\\ \\
&= 63 \cdot -\frac{1}{2}\sqrt{3}\\ \\
&= -\frac{63}{2}\sqrt{3}
\end{aligned}\]

New example

Orthogonal projection on a plane Suppose that \(\mathcal{V}\) is a plane through the origin and spanned by two orthogonal direction vectors \(\vec{v}\) and \(\vec{w}\). Then you can compute the projection of \(\vec{u}\) on \(\mathcal{V}\) as linear combination of \(\vec{v}\) and \(\vec{w}\): \[\text{proj}_{\mathcal{V}}(\vec{u}) = \left(\frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\vec{v}\boldsymbol{\cdot}\vec{v}}\right)\vec{v} + \left(\frac{\vec{u}\boldsymbol{\cdot}\vec{w}}{\vec{w}\boldsymbol{\cdot}\vec{w}}\right)\vec{w}\]