Inproduct, hoek en loodrechte projectie

Vectoren: Afstand, hoek, inproduct en uitproduct

Inproduct, hoek en loodrechte projectie

Standaarinproduct in 2D en 3D

Het standaardinproduct van de vectoren \(\vec{u}=\cv{u_1\\ u_2}\) en \(\vec{v}=\cv{v_1\\ v_2}\) in het coördinatenvlak \(\mathbb{R}^2\) definiëren we als \[\vec{u}\boldsymbol{\cdot}\vec{v}=u_1\cdot v_1+u_2\cdot v_2 \]

Het standaardinproduct van de vectoren \(\vec{u}=\cv{u_1\\ u_2\\ u_3}\) en \(\vec{v}=\cv{v_1\\ v_2\\v_3}\) in het coördinatenvlak \(\mathbb{R}^3\) definiëren we als \[\vec{u}\boldsymbol{\cdot}\vec{v}=u_1\cdot v_1+u_2\cdot v_2+ u_3\cdot v_3\]

Voorbeelden

\[\begin{aligned}\cv{2\\3}\boldsymbol{\cdot}\cv{4\\5}&=2\cdot 4+3\cdot 5\\ &=8+15=23\\ \\ \cv{2\\3}\boldsymbol{\cdot}\cv{3\\-2}&=2\cdot 3+3\cdot -2\\ &=6-6=0\\ \\ \cv{2\\3\\4}\boldsymbol{\cdot}\cv{5\\6\\-7}&=2\cdot 5+3\cdot 6+4\cdot -7=0\end{aligned}\]

Dit laat zich generaliseren tot de \(n\)-dimensionale coördinatenruimte \(\mathbb{R}^n\):

Standaardinproduct Het standaardinproduct van twee vectoren \(\vec{u}=\cv{u_1\\ \vdots \\ u_n}\) en \(\vec{v}=\cv{v_1\\ \vdots \\ v_n}\) in de \(n\)-dimensionale ruimte \(\mathbb{R}^n\), ook wel standaard inwendig product of scalair product genoemd, wordt gedefinieerd als \[\vec{u}\boldsymbol{\cdot}\vec{v}=u_1\cdot v_1+u_2\cdot v_2 +\cdots+ u_n\cdot v_n=\sum_{i=1}^n u_i\cdot v_i\]

We schrijven standaard inproduct en standaard inwendig product omdat in de coördinatenruimte ook andere inproducten gedefinieerd kunnen worden. Bijvoorbeeld kun je in \(\mathbb{R}^2\) ook het inproduct \[\vec{u}\boldsymbol{\cdot} \vec{v}=u_1v_1-u_1v_2-u_2v_1+3u_2v_2\] definiëren en deze heeft dan soortgelijke eigenschappen als het standaardinproduct.

Merk op dat voor een vector \(\vec{v}\) in \(\mathbb{R}^n\) geldt dat \[\lVert \vec{v}\rVert^2=\vec{v}\boldsymbol{\cdot} \vec{v}\]

Meestal spreken we gewoon van het inproduct, inwendig product of scalair product als we het standaardinproduct bedoelen en er geen verwarring is. De Engelstalige benaming dot product voor inproduct verklaart onze keuze van notatie met een vetgedrukte punt. Andere veelgebruikte notaties die je in boeken en artikelen tegen kunt komen zijn \(\langle \vec{u},\vec{v}\rangle\), \((\vec{u},\vec{v})\), \((\vec{u}\vert\vec{v})\) en \(\langle\vec{u}\vert\vec{v}\rangle\).

Bereken exact het volgende inproduct van vectoren \[\cv{8\\ 5} \boldsymbol{\cdot} \cv{-6\\ 2}\]

\(\cv{8\\ 5} \boldsymbol{\cdot} \cv{-6\\ 2}={}\)\( -38 \)

Immers: \[\begin{aligned} \cv{8\\ 5}\boldsymbol{\cdot}\cv{-6\\ 2} &= (8\cdot -6) + (5 \cdot 2) &\blue{\text{definitie van inproduct}} \\ &=-38 &\blue {\text{eindresultaat}} \end{aligned}\]

Nieuw voorbeeld

Eigenschappen van het inproduct Het inproduct op \(\mathbb{R}^n\) heeft de volgende eigenschappen voor alle scalairen \(\alpha\) en \(\beta\), en voor alle vectoren \(\vec{u}\), \(\vec{v}\), en \(\vec{w}\):

Symmetrie: \(\vec{u}\boldsymbol{\cdot} \vec{v} = \vec{v}\boldsymbol{\cdot} \vec{u}\)
Lineariteit: \(\left(\alpha\,\vec{u}+\beta\,\vec{v}\right)\boldsymbol{\cdot} \vec{w} = \alpha\,\vec{u}\boldsymbol{\cdot} \vec{w}+\beta\,\vec{v}\boldsymbol{\cdot} \vec{w}\)
Norm: \(\vec{v}\boldsymbol{\cdot} \vec{v}\ge 0\) en \(\vec{v}\boldsymbol{\cdot} \vec{v}= 0\iff \vec{v}=\vec{0}\). Daarom kun je een norm definiëren als \(\lVert\vec{v}\rVert=\sqrt{\vec{v}\boldsymbol{\cdot} \vec{v}}\).

Alle eigenschappen zijn voor \(\mathbb{R}^2\), \(\mathbb{R}^3\) en \(\mathbb{R}^n\) te bewijzen door het uitschrijven van de uitdrukkingen in coördinaten en het toepassen van de coördinaatsgewijze definities van optelling en scalaire vermenigvuldiging.

De genoemde eigenschappen zijn precies wat nodig is om van een vectorruimte \(V\) m.b.v. van een inproduct \(\boldsymbol{\cdot} : V\times V\longrightarrow \mathbb{R}\) tot een zogeheten inproductruimte te komen.

Bijvoorbeeld vormt de verzameling van reële continue functies op het interval \([0,1]\) met de gebruikelijke optelling en scalaire vermenigvuldiging een vectorruimte waarop we een inproduct kunnen definiëren als \[f\boldsymbol{\cdot}g = \int_0^1 f(x)\cdot g(x)\,dx\]

Gegeven dat het inproduct \(\vec{u}\boldsymbol{\cdot} \vec{v}= -2\), wat is dan de exacte waarde van het inproduct \(\left(-3\vec{u}\right)\boldsymbol{\cdot}\left( -2\vec{v}\right)\,\)?

\(\left(-3\vec{u}\right)\boldsymbol{\cdot}\left( -2\vec{v}\right)={}\)\(-12\).

Immers, gebruikmaking van de eigenschappen van het inproduct leidt tot \[\begin{aligned}\left(-3\vec{u}\right)\boldsymbol{\cdot}\left( -2\vec{v}\right) &= -3\cdot -2 \cdot \left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)\\ &=
6\cdot\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)\\
&=6\cdot -2\\
&=-12\\
\end{aligned}\]

Nieuw voorbeeld

Meetkundige betekenis van inproduct Het inproduct op het vlak \(\mathbb{R}^2\) en de ruimte \(\mathbb{R}^3\) heeft de volgende meetkundige betekenis:

Het inproduct \(\vec{u}\boldsymbol{\cdot}\vec{v}\) van twee vectoren \(\vec{u}\) en \(\vec{v}\) is gelijk aan het product van de lengte van \(\vec{u}\) en de lengte van de projectie van \(\vec{v}\) op de drager van \(\vec{u}\).

Anders geformuleerd: de loodrechte projectie van vector \(\vec{v}\) op de drager van vector \(\vec{u}\) is gelijk aan \(\left(\frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\vec{u}\boldsymbol{\cdot}\vec{u}}\right)\vec{u}\).

Onder referentie naar onderstaande figuur hebben we de volgende formule: \[\vec{u}\boldsymbol{\cdot}\vec{v} = \lVert\vec{u}\rVert\cdot\lVert\vec{v}\rVert\cdot\cos\phi\tiny.\]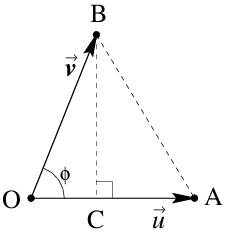

Met behulp van bovenstaande eigenschappen van het inproduct kunnen we \(\lVert\vec{u}-\vec{v}\rVert^2\) als volgt berekenen: \[\begin{aligned}\lVert\vec{u}-\vec{v}\rVert^2 &= (\vec{u}-\vec{v})\boldsymbol{\cdot} (\vec{u}-\vec{v})\\ &= \vec{u}\boldsymbol{\cdot}\vec{u} - 2\,\vec{u}\boldsymbol{\cdot}\vec{v}+ \vec{v}\boldsymbol{\cdot}\vec{v}\\ &= \lVert\vec{u}\rVert^2+\lVert\vec{v}\rVert^2-2\,\vec{u}\boldsymbol{\cdot}\vec{v}\tiny.\end{aligned}\] We kunnen \(\lVert\vec{u}-\vec{v}\rVert^2\) ook rechtstreeks berekenen. Laat \(\phi\) de hoek tussen de twee vectoren \(\vec{u}\) en \(\vec{v}\) zijn, waarbij \(0\le \phi\le \pi\). De eindpunten van de vectoren \(\vec{u}\) en \(\vec{v}\) noemen we \(A\) respectievelijk \(B\). Vanuit \(B\) laten we een loodlijn neer welke de drager van \(\vec{u}\) in \(C\) snijdt.

Verder geldt: \(\text{lengte van lijnstuk }BC=\lVert\vec{v}\rVert\sin\phi\) en \(\text{lengte van lijnstuk }OC=\lVert\vec{v}\rVert\cos\phi\). We kunnen nu \(\lVert\vec{u}-\vec{v}\rVert^2\) berekenen met behulp van de stelling van Pythagoras: \[\begin{aligned} \lVert\vec{u}-\vec{v}\rVert^2 &= \lVert\vec{AB}\rVert^2=\lVert\vec{BC}\rVert^2+\lVert\vec{CA}\rVert^2= \lVert\vec{BC}\rVert^2+\left(\lVert\vec{OA}\rVert-\lVert\vec{OC}\rVert\right)^2\\ &= \lVert\vec{v}\rVert^2\sin^2\!\phi+\left(\lVert\vec{u}\rVert-\lVert\vec{v}\rVert\cos\phi\right)^2 \\ &= \lVert\vec{u}\rVert^2+ \lVert\vec{v}\rVert^2\left(\sin^2\!\phi+\cos^2\!\phi\right)-2\,\lVert\vec{u}\rVert\,\lVert\vec{v}\rVert\,\cos\phi \\ &= \lVert\vec{u}\rVert^2 + \lVert\vec{v}\rVert^2-2\,\lVert\vec{u}\rVert\,\lVert\vec{v}\rVert\,\cos\phi\end{aligned}\] Vergelijken we de twee uitdrukkingen voor \(\lVert\vec{u}-\vec{v}\rVert^2\), dan vinden we \[\vec{u}\boldsymbol{\cdot}\vec{v} = \lVert\vec{u}\rVert\,\lVert\vec{v}\rVert\,\cos\phi\]

Omgekeerd kunnen we met behulp van het inproduct een hoek tussen twee vectoren definiëren.

Hoek tussen twee vectoren De (korte) hoek \(\phi\) tussen twee vectoren \(\vec{u}\) en \(\vec{v}\), beiden ongelijk aan de nulvector, wordt gedefinieerd door de formule \[\cos(\phi) = \frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\lVert\vec{u}\rVert\cdot\lVert\vec{v}\rVert}\qquad (\text{met }0\le \phi\le \pi)\] Deze hoek is scherp als \(\vec{u}\boldsymbol{\cdot}\vec{v}>0\), en stomp als \(\vec{u}\boldsymbol{\cdot}\vec{v}<0\).

Verder zien we dat \(\vec{u}\boldsymbol{\cdot}\vec{v}=0\) precies betekent dat de vectoren \(\vec{u}\) en \(\vec{v}\) loodrecht op elkaar staan. We zeggen ook wel dat de vectoren \(\vec{u}\) en \(\vec{v}\) orthogonaal zijn.

De volgende ongelijkheid is in vlak \(\mathbb{R}^2\) en ruimte \(\mathbb{R}^3\) nu evident. Deze ongelijkheid, en daarmee ook het begrip hoek, laat zich generaliseren tot \(\mathbb{R}^n\).

Cauchy-Schwarz ongelijkheid Voor alle vectoren \(\vec{u}\) en \(\vec{v}\) in \(\mathbb{R}^n\) geldt \[\left|\vec{u}\boldsymbol{\cdot}\vec{v}\right|\le \lVert\vec{u}\rVert\cdot\lVert\vec{v}\rVert\]

In feite geldt de ongelijkheid van Cauchy-Schwarz voor elke inproductruimte. In het bewijs hoeven we alleen eigenschappen van het inproduct toe te passen.

Als \(\vec{v}=\vec{0}\), dan is de bewering juist. We mogen dus aannemen dat \(\vec{v}\neq\vec{0}\) en introduceren het getal \(\lambda=\frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\lVert\vec{v}\rVert^2}\). Dan geldt: \[\begin{aligned}0&\leq \lVert\vec{u}-\lambda\vec{v}\rVert^2 \\ \\ &= \left(\vec{u}-\lambda\vec{v}\right) \boldsymbol{\cdot}\left(\vec{u}-\lambda\vec{v}\right) \\ \\ &= \vec{u}\boldsymbol{\cdot}\vec{u} - 2\lambda\vec{u}\boldsymbol{\cdot}\vec{v}+\lambda^2\vec{v}\boldsymbol{\cdot}\vec{v} \\ \\ &= \lVert\vec{u}\rVert^2-\frac{\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)^2}{\lVert\vec{v}\rVert^2}\end{aligned}\] Dus \[ \frac{\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)^2}{\lVert\vec{v}\rVert^2}\le \lVert\vec{u}\rVert^2\] oftewel \[\left|\vec{u}\boldsymbol{\cdot}\vec{v}\right|\le \lVert\vec{u}\rVert\cdot \lVert\vec{v}\rVert\tiny.\]

De vector \(\vec{u}\) heeft lengte \(2\) en de vector \(\vec{v}\) heeft lengte \(4\). De hoek tussen de twee vectoren is gelijk aan \(90^{\circ}\).

Wat is de exacte waarde van het inproduct \(\vec{u}\boldsymbol{\cdot} \vec{v}\,\)?

\(\vec{u}\boldsymbol{\cdot}\vec{v}={}\)\(0\)

Immers, als \(\phi\) de hoek tussen de vectoren \(\vec{u}\) en \(\vec{v}\) is, dan geldt \[\begin{aligned}\vec{u}\boldsymbol{\cdot}\vec{v} &= \lVert\vec{u}\rVert\cdot\lvert\vec{v}\rvert\cdot \cos(\phi)\\ \\
&= 2 \cdot 4 \cdot\cos\left(90^{\circ}\right)\\ \\
&= 8 \cdot 0\\ \\
&= 0
\end{aligned}\]

Nieuw voorbeeld

Orthogonale projectie op een plat vlak Stel dat \(\mathcal{V}\) een plat vlak in de ruimte is door de oorsprong opgespannen door twee orthogonale richtingsvectoren \(\vec{v}\) en \(\vec{w}\). Dan kun je de projectie van \(\vec{u}\) op het vlak \(\mathcal{V}\) berekenen als lineaire combinatie van \(\vec{v}\) en \(\vec{w}\): \[\text{proj}_{\mathcal{V}}(\vec{u}) = \left(\frac{\vec{u}\boldsymbol{\cdot}\vec{v}}{\vec{v}\boldsymbol{\cdot}\vec{v}}\right)\vec{v} + \left(\frac{\vec{u}\boldsymbol{\cdot}\vec{w}}{\vec{w}\boldsymbol{\cdot}\vec{w}}\right)\vec{w}\]