Normal vector and cross product in ℝ³

Vectors: Distance, angle, dot product and cross product

Normal vector and cross product in ℝ³

The term normal vector is also applicable to surfaces in \(\mathbb{R}^3\).

Normal equation of a plane Consider in \(\mathbb{R}^3\) a plane \(\mathcal{V}\) and let \(d\) be the distance from the origin \(O\) to \(\mathcal{V}\). Let \(\vec{n}\) a vector of length \(1\) that is perpendicular to \(\mathcal{V}\) and point toward \(\mathcal{V}\): \(\vec{n}\) is called a normal vector to the plane \(\mathcal{V}\).

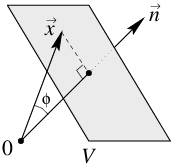
By the length choice of the normal vector \(\vec{n}\) we can determine whether the terminal point of a vector \(\vec{x}\) lies on the plane \(\mathcal{V}\): a necessary and sufficient condition is that the projection of \(\vec{x}\) on the span of \(\vec{n}\) has length \(d\). The formula is: \[\text{terminal point of }\vec{x}\text{ on }\mathcal{V}\iff \lVert\vec{x}\rVert\cdot \cos(\phi)=d\iff \vec{n}\boldsymbol{\cdot}\vec{x}=d\tiny.\] In terms of coordinates we get \[n_1x_1+n_2x_2+n_3x_3=d\tiny.\] This is called a normal equation of the plane \(\mathcal{V}\). When we multiply the left- and right-hand side with the same number, we also get a normal equation of the plane, but we have lost the special role of the constant on the right-hand side.

The reason for the naming is the same as in \(\mathbb{R}^2\): if \(\vec{a}\) is a support vector of the plane \(\mathcal{V}\), then the equation \[\vec{n}\boldsymbol{\cdot}\left(\vec{x}-\vec{a}\right)=0\] represents the plane \(\mathcal{V}\).

Notation Again, we mostly do not use in plane geometry for general points the coordinates \((x_1,x_2,x_3)\), but instead we write \((x,y,z)\). The general form of an equation of a plane \(\mathcal{V}\) is then \(ax+by+cz=d\), where \(\vec{n}=\cv{a\\b\\c}\) is a normal vector of this plane (not necessarily, of length \(1\)).

We commonly abbreviate 'normal equation' to 'equation'. The distinction with a vector representation of a plane is already clear enough in the naming. Sometimes one uses the term vector equation of a plane instead of vector representation, but again the extended name vector equation is already clear enough to recognize the distinction with an equation.

Formulas for distance Two surfaces \(\mathcal{V}\) and \(\mathcal{W}\) in \(\mathbb{R}^3\) with the same normal vector \(\vec{n}\) are parallel or coinciding planes. If \(\vec{a}\) is a vector with the terminal point on \(\mathcal{V}\) and \(\vec{b}\) is a vector with the terminal point on \(\mathcal{W}\), then the distance \(d(\mathcal{V},\mathcal{W})\) between the two planes can be calculated via the formula \[d(\mathcal{V},\mathcal{W})=\frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert}\] The same formula also gives the shortest distance from the terminal point of \(\vec{b}\) to the plane \(\mathcal{V}\): \[d(V,\vec{b})=\frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert}\]

The proof is similar to the one for straight lines in a plane: \(\left(\frac{\vec{n}\boldsymbol{\cdot} \vec{a}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right) \vec{n}\) is the projection of \(\vec{a}\) on the span of \(\vec{n}\). Similarly, \(\left(\frac{\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right) \vec{n}\) is the projection of \(\vec{b}\) on the span of \(\vec{n}\). The distance between the terminal points of these two vectors is equal to the distance \(d(\mathcal{V},\mathcal{W})\) between the two planes \(\mathcal{V}\) and \(\mathcal{W}\). This distance is the length of the difference vector of the two projections, and is thus equal to \[\begin{aligned} d(\mathcal{V},\mathcal{W}) &= \left\lVert \frac{\vec{n}\boldsymbol{\cdot} \vec{a}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\,\vec{n}-\frac{\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\, \vec{n}\right\rVert \\ \\ &= \left\lVert \left(\frac{\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right) \vec{n}\right\rVert \\ \\ &= \left| \frac{\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right|\cdot \lVert\vec{n}\rVert \\ \\ & \frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert^2}\cdot \lVert\vec{n}\rVert \\ \\&= \frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert}\end{aligned}\] Because the projection on the span of \(\vec{n}\) does not depend on the choice of \(\vec{b}\) on the plane \(\mathcal{W}\) we may also use the formula for a randomly selected point. In fact, we say that the distance from a point \(P\) to a plane \(\mathcal{V}\) is by definition equal to the distance between the plane \(\mathcal{V}\) and the plane which is parallel to \(\mathcal{V}\) and that goes through \(P\).

The point \( (1,4,c) \) lies on the plane \( \mathcal{V} \) given by the equation \[x-4y+3z=-12\] What is the exact value of \( c \) ?

\(c={} \)\(1 \)

The given point must satisfy the equation of the plane \( \mathcal{V}:x -4y +3z=-12 \).
Substitution of the coordinates of the point \( (1,4,c)\) into the equation gives: \[1\cdot1-4\cdot4+3\cdot c=-12\tiny.\] Thus: \[1-16+3 c=-12\tiny.\] Moving all constants to the right-hand side leads to: \[\begin{aligned} 3 c &= -12-1+16 \\
&= 3\end{aligned}\] \(\text{This means that } c=\frac{3}{3}=1 \)

New example

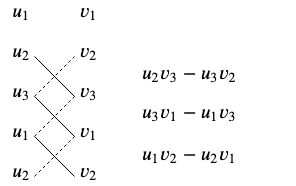
Cross product The cross product of two vectors \(\vec{u}=\cv{u_1\\u_2\\ u_3}\) and \(\vec{v}=\cv{v_1\\ v_2\\ v_3}\) in the \(3\)-dimensional space \(\mathbb{R}^3\) is defined as \[\vec{u}\times \vec{v}=\cv{u_2v_3-u_3v_2\\ u_3v_1-u_1v_3\\ u_1v_2-u_2v_1}\]

Do not confuse the cross product of vectors with the Hadamard product of vectors defined by componentwise multiplication \[\vec{u}\ast\vec{v}=\cv{u_1v_1\\ u_2v_2\\ u_3v_3}\]

Mnemonics The definition of the cross product can be remembered as follows. Write: \(\begin{vmatrix}a&b\\c&d\end {vmatrix} = ad-bc \). The left-hand side is called a determinant. The components of \(\vec{u}\boldsymbol{\times}\vec{v}\) are the determinants that we can form out of \(\begin{pmatrix} u_1 & v_1\\ u_2 & v_2\\ u_3 & v_3\end {pmatrix} \) by successively leaving out the first, the second and the third row, and by attributing the signs \(+\), \(-\), and \(+\), respectively.

Another, related mnemonic is the construction visualized below. Under each vector, write the first two components of that vector. Ignore the top line and consider downwards each block of four components: subtract the product of the components connected by a dashed line from the product of the components connected by a solid line.

mnemonic forr the definition of the cross product

Properties of the cross product For all \(\vec{u}, \vec{v}, \vec{w}\in\mathbb{R}^3\) and all \(\lambda\in \mathbb{R}\) we have:

\(\;\vec{u}\times\vec{u}=0\).
\(\;\vec{u}\times\vec{v}=-\vec{v}\times\vec{u}\).
\(\;\vec{u}\times\left(\vec{v}+\vec{w}\right)=\left(\vec{u}\times\vec{v}\right) + \left(\vec{u}\times\vec{w}\right)\).
\(\;\left(\vec{u}+\vec{v}\right)\times \vec{w}=\left(\vec{u}\times\vec{w}\right) + \left(\vec{v}\times\vec{w}\right)\).
\(\;\lambda\left(\vec{u}\times\vec{v}\right)=\left(\lambda\vec{u}\right)\times\vec{v}= \vec{u}\times\left(\lambda\vec{v}\right)\).
\(\;\left(\vec{u}\times\vec{v}\right) \boldsymbol{\cdot} \vec{u} = \left(\vec{u}\times\vec{v}\right) \boldsymbol{\cdot} \vec{v}=0\).
\(\;\lVert \vec{u}\times\vec{v}\rVert=\Vert \vec{u}\rVert\cdot\Vert \vec{v}\rVert\cdot|\sin\phi|\), where \(\phi\) is the angle between the two vectors \(\vec{u}\) and \(\vec{v}\).

Especially property (f) is useful, for example, to determine a normal vector on the basis of two direction vectors of a plane. This is also an easy way to compute an equation of a plane for which a vector representation is already known.

The properties (a) up to and including (f) of the cross product are easy to prove by writing them out in terms of coordinates. Verifying property \(g\) requires more handwriting: \[\begin{aligned} \lVert \vec{u}\times\vec{v}\rVert^2 &= \left(\vec{u}\times\vec{v}\right)\boldsymbol{\cdot}\left(\vec{u}\times\vec{v}\right) \\ &= (u_2v_3-u_3v_1)^2+(u_3v_1-u_1v_3)^2 +(u_1v_2-u_2v_1)^2\\ &= \left(\vec{u}\boldsymbol{\cdot}\vec{u}\right)\cdot\left(\vec{v}\boldsymbol{\cdot}\vec{v}\right)-\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)^2\qquad\blue{\text{(can be verified by working out)}}\\ &= \lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2- \lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2\cdot \cos^2\!\phi\\ &=\lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2\cdot \left(1-\cos^2\!\phi\right)\\ &= \lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2 \cdot\sin^2\!\phi\end{aligned}\]

Calculate the cross product \(\cv{-2\\5\\-5} \times \cv{-2\\0\\2} \)

\(\cv{-2\\5\\-5} \times \cv{-2\\0\\2} ={}\) \(\cv{10\\14\\10}\)

After all: \[\begin{aligned} \cv{-2\\5\\-5} \times \cv{-2\\0\\2} &= \cv{5 \cdot 2 +5 \cdot 0 \\ -5\cdot -2 +2 \cdot 2\\ -2\cdot 0 - 5\cdot -2}
&{\blue{\text{definition of cross product}}}\\
&=\cv{10\\14\\10}
&{\blue{\text{simplification}}}
\end{aligned}\]

New example