Normaalvector van een vlak in ℝ3 en het uitproduct

Vectoren: Afstand, hoek, inproduct en uitproduct

Normaalvector van een vlak in ℝ³ en het uitproduct

Het begrip normaalvector is ook toepasbaar voor vlakken in \(\mathbb{R}^3\).

Normaalvergelijking van een vlak Beschouw in \(\mathbb{R}^3\) een vlak \(\mathcal{V}\) en laat \(d\) de afstand zijn van de oorsprong \(O\) tot \(\mathcal{V}\). Laat \(\vec{n}\) een vector van lengte \(1\) zijn die loodrecht staat op \(\mathcal{V}\) en naar \(\mathcal{V}\) wijst: \(\vec{n}\) heet een normaalvector van het vlak \(\mathcal{V}\).

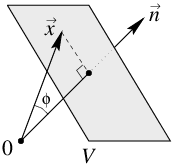
Door de lengtekeuze van de normaalvector \(\vec{n}\) kunnen we vaststellen of het eindpunt van een vector \(\vec{x}\) op het vlak \(\mathcal{V}\) ligt: een noodzakelijke en voldoende voorwaarde is dat de projectie van \(\vec{x}\) op de drager van \(\vec{n}\) lengte \(d\) heeft. In formulevorm: \[\text{eindpunt van }\vec{x}\text{ op }\mathcal{V}\iff \lVert\vec{x}\rVert\cdot \cos(\phi)=d\iff \vec{n}\boldsymbol{\cdot}\vec{x}=d\tiny.\] Uitgeschreven in coördinaten hebben we \[n_1x_1+n_2x_2+n_3x_3=d\tiny.\] Dit heet een normaalvergelijking van het vlak \(\mathcal{V}\). Als we links en rechts met eenzelfde getal vermenigvuldingen krijgen we ook een normaalvergelijking van het vlak, maar is de bijzondere rol van de constante aan de rechterkant verloren gegaan.

De reden voor de naamgeving is gelijk aan die in \(\mathbb{R}^2\): als \(\vec{a}\) een steunvector van het vlak \(\mathcal{V}\) is, dan stelt de vergelijking \[\vec{n}\boldsymbol{\cdot}\left(\vec{x}-\vec{a}\right)=0\] het vlak \(\mathcal{V}\) voor.

Notatieconventie Ook nu weer gebruiken we meestal in de vlakke meetkunde voor algemene punten niet de coördinaten \((x_1,x_2,x_3)\), maar schrijven we \((x,y,z)\). De algemene vorm van een vergelijking van een vlak \(\mathcal{V}\) is dan \(ax+by+cz=d\), waarbij \(\vec{n}=\cv{a\\b\\c}\) een normaalvector van dit vlak is (niet noodzakelijkwijs met lengte \(1\)).

Ook korten we normaalvergelijking meestal af tot vergelijking. Het onderscheid met een vectorvoorstelling van een vlak is al helder genoeg in de naamgeving. Soms gebruikt men de term vectorvergelijking van een vlak i.p.v. vectorvoorstelling, maar ook dan is de verlengde naam vectorvergelijking al duidelijk genoeg om het onderscheid met een vergelijking te herkennen.

Formules voor afstand Twee vlakken \(\mathcal{V}\) en \(\mathcal{W}\) in \(\mathbb{R}^3\) met dezelfde normaalvector \(\vec{n}\) zijn parallelle of samenvallende vlakken. Als \(\vec{a}\) een vector is met het eindpunt op \(\mathcal{V}\) en \(\vec{b}\) een vector is met het eindpunt op \(\mathcal{W}\), dan kan de de afstand \(d(\mathcal{V},\mathcal{W})\) tussen de twee vlakken berekend worden met de formule \[d(\mathcal{V},\mathcal{W})=\frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert}\] Dezelfde formule geeft ook de kortste afstand van het eindpunt van \(\vec{b}\) tot het vlak \(\mathcal{V}\): \[d(V,\vec{b})=\frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert}\]

Het bewijs verloopt net als eerder voor rechte lijnen in een vlak: \(\left(\frac{\vec{n}\boldsymbol{\cdot} \vec{a}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right) \vec{n}\) is de projectie van \(\vec{a}\) op de drager van \(\vec{n}\). Evenzo is \(\left(\frac{\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right) \vec{n}\) de projectie van \(\vec{b}\) op de drager van \(\vec{n}\). De afstand tussen de eindpunten van deze twee vectoren is dan gelijk de afstand \(d(\mathcal{V},\mathcal{W})\) tussen de twee vlakken \(\mathcal{V}\) en \(\mathcal{W}\). Deze afstand is de lengte van de verschilvector van de twee projecties en dus gelijk aan \[\begin{aligned} d(\mathcal{V},\mathcal{W}) &= \left\lVert \frac{\vec{n}\boldsymbol{\cdot} \vec{a}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\,\vec{n}-\frac{\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\, \vec{n}\right\rVert \\ \\ &= \left\lVert \left(\frac{\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right) \vec{n}\right\rVert \\ \\ &= \left| \frac{\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}}{\vec{n}\boldsymbol{\cdot} \vec{n}}\right|\cdot \lVert\vec{n}\rVert \\ \\ & \frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert^2}\cdot \lVert\vec{n}\rVert \\ \\&= \frac{\left|\vec{n}\boldsymbol{\cdot} \vec{a}-\vec{n}\boldsymbol{\cdot} \vec{b}\right|}{\lVert\vec{n}\rVert}\end{aligned}\] Omdat de projectie op de drager van \(\vec{n}\) niet afhangt van de keuze van \(\vec{b}\) op het vlak \(\mathcal{W}\) mogen we de formule ook gebruiken voor een willekeurig gekozen punt. In feite zeggen we dan dat de afstand van een punt \(P\) tot een vlak \(\mathcal{V}\) per definitie gelijk is aan de afstand tussen het vlak \(\mathcal{V}\) en het vlak dat parallel aan \(\mathcal{V}\) is en door \(P\) gaat.

Het punt \( (2,5,c) \) ligt op het vlak \( \mathcal{V} \) gegeven door de vergelijking \[4x +4y +5z=3\] Wat is de exacte waarde van \(c \) ?

\(c={}\)\(-5 \)

Het gegeven punt in het vlak moet voldoen aan de vergelijking voor het vlak \( 4x +4y +5z=3 \).
Invullen van de coördinaten van \( (2,5,c)\) in de vergelijking geeft \[4\cdot2+4\cdot5+5\cdot c=3\tiny. \] Oftewel \[8+20+5 c=3\tiny.\] Nu halen we de constanten naar rechts: \[\begin{aligned} 5 c &= 3-8-20 \\
&= -25\end{aligned}\] \(\text{Dus }c=\frac{-25}{5}=-5\)

Nieuw voorbeeld

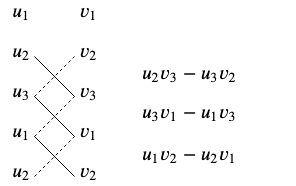
Standaarduitproduct Het standaarduitproduct van twee vectoren \(\vec{u}=\cv{u_1\\u_2\\ u_3}\) en \(\vec{v}=\cv{v_1\\ v_2\\ v_3}\) in de \(3\)-dimensionale ruimte \(\mathbb{R}^3\), ook wel standaard uitwendig product of kruisproduct genoemd, wordt gedefinieerd als \[\vec{u}\times \vec{v}=\cv{u_2v_3-u_3v_2\\ u_3v_1-u_1v_3\\ u_1v_2-u_2v_1}\]

Verwar het standaarduitproduct van vectoren niet met het Hadamard product van vectoren, gedefinieerd door componentsgewijze vermenigvuldiging \[\vec{u}\ast\vec{v}=\cv{u_1v_1\\ u_2v_2\\ u_3v_3}\]

Ezelbruggetjes De definitie van het standaarduitproduct kunnen we als volgt onthouden. Schrijf: \(\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bc\). Het linkerlid heet een determinant. De componenten van \(\vec{u}\boldsymbol{\times}\vec{v}\) zijn de determinanten die we uit \(\begin{pmatrix} u_1 & v_1\\ u_2 & v_2\\ u_3 & v_3\end{pmatrix}\) kunnen vormen door achtereenvolgens de eerste, de tweede en de derde rij weg te laten, voorzien van de tekens \(+\), \(-\), resp. \(+\).

Een hiermee gerelateerd ezelbruggetje is de constructie die hieronder gevisualiseerd is. Onder elke vector schrijf je de eerste twee componenten van die vector. Laat de eerste rij links liggen en beschouw van boven naar beneden steeds een blok van 4 componenten: trek de producten van de componenten verbonden met een stippellijn af van het product van de componenten verbonden met een doorgetrokkken lijn.

ezelsbruggetje voor uitproduct

Eigenschappen van het uitproduct Voor alle \(\vec{u}, \vec{v}, \vec{w}\in\mathbb{R}^3\) en alle \(\lambda\in \mathbb{R}\) geldt:

\(\;\vec{u}\times\vec{u}=0\).
\(\;\vec{u}\times\vec{v}=-\vec{v}\times\vec{u}\).
\(\;\vec{u}\times\left(\vec{v}+\vec{w}\right)=\left(\vec{u}\times\vec{v}\right) + \left(\vec{u}\times\vec{w}\right)\).
\(\;\left(\vec{u}+\vec{v}\right)\times \vec{w}=\left(\vec{u}\times\vec{w}\right) + \left(\vec{v}\times\vec{w}\right)\).
\(\;\lambda\left(\vec{u}\times\vec{v}\right)=\left(\lambda\vec{u}\right)\times\vec{v}= \vec{u}\times\left(\lambda\vec{v}\right)\).
\(\;\left(\vec{u}\times\vec{v}\right) \boldsymbol{\cdot} \vec{u} = \left(\vec{u}\times\vec{v}\right) \boldsymbol{\cdot} \vec{v}=0\).
\(\;\lVert \vec{u}\times\vec{v}\rVert=\Vert \vec{u}\rVert\cdot\Vert \vec{v}\rVert\cdot|\sin\phi|\), waarbij \(\phi\) de hoek is tussen de twee vectoren \(\vec{u}\) en \(\vec{v}\).

Vooral eigenschap (f) is handig om bijvoorbeeld, gegeven twee richtingsvectoren van een vlak, een normaalvector te bepalen. Dit is ook een korte manier om gegeven een vectorvoorstelling van een vlak in de driedimensionale ruimte een bijpassende vergelijking op te stellen.

De eigenschappen (a) t/m (f) van het uitproduct zijn eenvoudig te bewijzen door ze uit te schrijven in coördinaten. Het verifiëren van eigenschap \(g\) vergt wat meer schrijfwerk: \[\begin{aligned} \lVert \vec{u}\times\vec{v}\rVert^2 &= \left(\vec{u}\times\vec{v}\right)\boldsymbol{\cdot}\left(\vec{u}\times\vec{v}\right) \\ &= (u_2v_3-u_3v_1)^2+(u_3v_1-u_1v_3)^2 +(u_1v_2-u_2v_1)^2\\ &= \left(\vec{u}\boldsymbol{\cdot}\vec{u}\right)\cdot\left(\vec{v}\boldsymbol{\cdot}\vec{v}\right)-\left(\vec{u}\boldsymbol{\cdot}\vec{v}\right)^2\qquad\blue{\text{(te verifiëren door uitwerking)}}\\ &= \lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2- \lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2\cdot \cos^2\!\phi\\ &=\lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2\cdot \left(1-\cos^2\!\phi\right)\\ &= \lVert \vec{u}\rVert^2\cdot \lVert \vec{v}\rVert^2 \cdot\sin^2\!\phi\end{aligned}\]

Bereken het uitproduct \(\cv{-4\\0\\3} \times \cv{-5\\-5\\-2} \)

\(\cv{-4\\0\\3} \times \cv{-5\\-5\\-2} ={}\)\(\cv{15\\-23\\20}\)

Immers: \[\begin{aligned} \cv{-4\\0\\3} \times \cv{-5\\-5\\-2} &= \cv{0 \cdot -2 - 3 \cdot -5 \\ 3\cdot -5 +4 \cdot -2\\ -4\cdot -5 - 0\cdot -5}
&{\blue{\text{definitie uitproduct}}}\\
&=\cv{15\\-23\\20}
&{\blue{\text{vereenvoudiging}}}
\end{aligned}\]

Nieuw voorbeeld