Addition, scalar multiplication and linear combination You can add vectors, multiply themby a scalar, and you can combine them. This is done in the way you might expect. The only remarkable thing about addition, but what turns out to be a pleasant side effect, is that you can also add/subtract a number to a vector by considering the number as a vector of appropriate length with all values equal to the given number so that the addition/subtraction has meaning.

>> u = [1; 2];  v = [3; 4];
>> u + v
ans =
     4
     6
>> 5*u
ans =
     5
    10
>> 5*u - 2*v
ans =
    -1
     2
>> u + 1
ans =
     2
     3

Multiplication, dot product, cross product, and the Hadamard product So far we have seen in the theory pages the inner product, the cross product and the Hadamard product. MATLAB facilitates these calculations:

>> clear all
>> u = [1;2;3]; v = [4;5;6];
>> innerproduct = dot(u, v)
innerproduct =
    32
>> crossproduct = cross(u, v)
crossproduct =
    -3
     6
    -3
>> Hadamard_product = u .* v
Hadamard_product =
     4
    10
    18
>> u*v
Error using  * 
Inner matrix dimensions must agree. 
>> u' * v  % another way to compute the inproduct of u and v
ans =
    32

What we learn from the above examplea is that the multiplication symbol * has a special meaning, namelymultiplication of matrices. MATLAB can consider the vectors as matrices with one column or one row, and the product of a row vector and column vector with the same dimension can then be calculated and considered as the inner product.

Arithmetic operations With a dot before the multiplication symbol, so with .* , you indicate that you want to apply multiplication componentwise. You can also do this with other arithmetic operators like division and exponentiation. In this way you can also quickly construct vectors that are defined by making indexing functions or make simple graphs of functions. We give some examples to illustrate this.

>> clear all
>> u = [3;4]; v = [5;6];
>> u ./ v    % componentwise division
ans =
    0.6000
    0.6667
>> u .^ 2    % componentwise exponentiation
ans =
     9
    16
>> sqrt(sum(u.^2))    % computation of the Euclidean norm of u
ans =
     5
>> i = 1:5;  v = 1 ./ (i + 1)    % v_i = 1/(i+1)
v =
    0.5000    0.3333    0.2500    0.2000    0.1667
>> t = 0:0.01:pi;
>> y = t - 1/6*t.^3 + 1/120*t.^5 - 1/5040*t.^7;
>> s = sin(t);
>> plot(t, s, '-b', t, y, '-r')   % sine graph (blue) and graph of a polynomial function (red)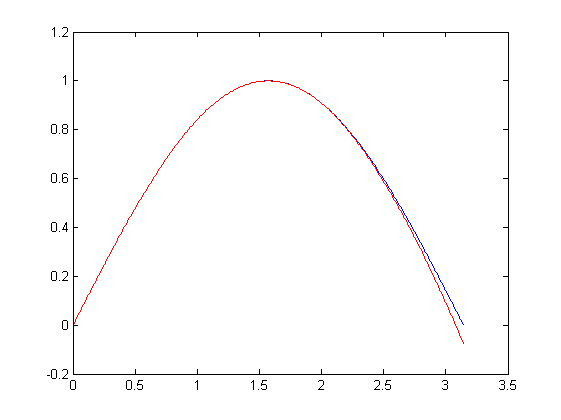

Vectorization The previous example of a sine graph also illustrates that MATLAB "understands" that the only meaningful use of mathematical functions on vectors is that they are used componentwise. This working style is called vectorization and makes the MATLAB language concise and clear. We give a few examples to illustrate this.

>> clear all
>> x = 1:5
x =
     1     2     3     4     5
>> sqrt(x)   % componentwise extraction of roots
ans =
    1.0000    1.4142    1.7321    2.0000    2.2361
>> log(x)    % componentwise application of the natural logarithm
ans =
         0    0.6931    1.0986    1.3863    1.6094
>> exp(x)    % componentwise application of the exponential function
ans =
    2.7183    7.3891   20.0855   54.5982  148.4132
>> clear all
>> i = 1:6;  v = (-1).^i ./ i  % v_i = (-1)^i/i
v =
   -1.0000    0.5000   -0.3333    0.2500   -0.2000    0.1667
>> minmax = [min(v) max(v) ]   % minimum and maximum
minmax =
   -1.0000    0.5000
>> sum(v)         % summation of all components
ans =
   -0.6167
>> cumsum(v)      % cumulative summation
ans =
   -1.0000   -0.5000   -0.8333   -0.5833   -0.7833   -0.6167
> sv = sign(v)    % signs of the components
sv =
    -1     1    -1     1    -1     1
>> dsv = diff(sv) % differences in consecutive signs
dsv =
     2    -2     2    -2     2
>> find(dsv>0)    % indices with transition from - to + sign in v
ans =
     1     3     5