Rij- en kolomvectoren en onbestemde vectoren Een vector, die naar gelang het gebruik als rij- of kolomvector worden opgevat, maak je door de getallen in een lijst te zetten en het als argument in de nparray functie te gebruiken. Het lijkt wel op een rijvector, maar is het niet echt.

Een rijvector of kolomvector krijg je wanneer je de componenten aanbiedt als een geneste lijst; dit is in feite een matrix met 1 rij of 1 kolom.

Hieronder staan achter de prompt in een interactieve Python sessie opdrachten om een vector. Een getransponeerde vector wordt verkregen door de methode transpose van een nparray object te gebruiken.

>>> np.array([1,2,3])  # vector
array([1, 2, 3])
>>> v = np.array([4, 5, 6]); print(v)  # printout van een vector
[4 5 6]
>>> print(v.transpose()) # getransponeeerde vector
[4 5 6]
>>> rv = np.array([[4, 5, 6]]); print(rv)  # rijvector
[[4 5 6]]
>>> kv = np.array([[4], [5], [6]]); print(kv)
[[4]
 [5]
 [6]]
>>> kv.transpose()  # getransponeeerde kolomvector
array([[4, 5, 6]])

Dimensie en norm Met de shape instructie kun je bepalen of het een rij- of kolomvector is. Met de size instructie kun je de dimensie van een vector achterhalen. De (Euclidische) lengte van een vector bereken je numeriek in Python met het commando norm en er zijn opties om varianten te berekenen

>>> v = np.array([4,5,6])
>>> type(v)
<class 'numpy.ndarray'>
>>> v.shape
(3,)
>>> np.size(v)
3
>>> print(kv)  # kolomvector
[[4]
[5]
[6]]
>>> la.norm(kv)    # Euclidische lengte
8.774964387392123
>>> la.norm(kv,1)  # som van absolute waarden van componenten
15.0
>>> la.norm(kv, np.inf)  # maximum van absolute waarden van componenten
6.0

Speciale constructievormen Verder zijn er speciale commando's om specifieke vectoren te maken; we tonen een paar veel gebruikte constructies.

>>> v1 = np.arange(5,11); print(v1)    # van 5 tot 11
[ 5 6 7 8 9 10]
>>> v2 = np.arange(10,4,-2); print(v2) # van 10 tot 4 met stapjes van -2
[10 8 6]
>>> v3 = np.linspace(0,1,6)  # gelijkmatige verdeling van 6 punten over [0,1]
>>> print(v3)
[0. 0.2 0.4 0.6 0.8 1. ]
>>> v4 = np.zeros((3,1), dtype=int);   # kolomvector met 3 nullen
>>> print(v4)
[[0]
 [0]
 [0]]
>>> v5 = np.ones((3,), dtype=bool)  # rijvector met logische waarden 1
>>> print(v5)
[ True, True, True]
>>> v6 = np.array([]); print(v6)
[]

Aan elkaar plakken van vectoren Je kunt ook nieuwe vectoren creëren door vectoren aan elkaar te plakken. Hiervoor kun je de functies concatenate, hstack en vstack gebruiken

>>> v1 = np.arange(1,4); v2 = np.arange(4,7); v12 = np.hstack((v1,v2))
>>> print(v12)
[1 2 3 4 5 6]
>>> np.concatenate((v1, v2))
array([1, 2, 3, 4, 5, 6])

Willekeurig gegenereerde vectoren In simulaties zullen we veel gebruik maken van vectoren met willekeurig gegenereerde getallen, in het Engels random number genoemd. Hiervoor zijn verschillende instructies:

>>> np.random.rand(5,1)
array([[0.60839603],
[0.08385416],
[0.18951417],
[0.0336493 ],
[0.3009523 ]])
>>> # 10 willekeurige gehele getallen tussen 5 en 8 (inclusief):
>>> np.random.randint(5, high=9, size=10) 
array([8, 8, 8, 7, 5, 8, 8, 7, 5, 6])
>>> # 5 willekeurige getallen volgens standaard normale verdeling:
>>> np.random.standard_normal(5)  
array([-0.48421341, 2.63156996, -0.28340041, -1.55714191, 0.69337535])
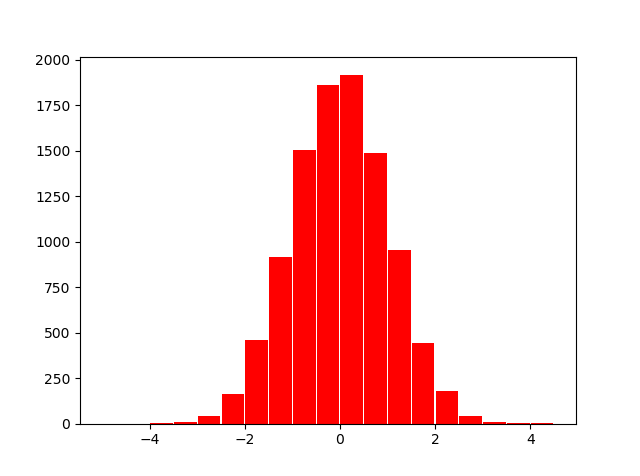
>>> x = np.arange(-5, 5, 0.5)
>>> y = np.random.standard_normal(10000)
>>> import matplotlib.pyplot as plt
>>> N, bins, patches = plt.hist(y,x,color='r', rwidth=0.95)
>>> plt.show()