We have previously seen in this chapter that \(2\times 2\) matrix \(A=\matrix{a_{11} & a_{12}\\ a_{21} & a_{22}}\) is invertible if and only if \(a_{11}a_{22}-a_{12}a_{21}\neq 0\). The term \(a_{11}a_{22}-a_{12}a_{21}\) is called the determinant of the matrix \(A\) and is denoted \(\text{det}(A)\).
The determinant of a #2\times 2# matrix
\[
A=\left(\begin{array}{cc} a & b \\ c & d \end{array}\right)
\]
is the number #a\cdot d-b\cdot c#.
Common notations for the determinant of #A# are #\det(A)# and \(
\left|\begin{array}{cc} a & b \\ c & d \end{array}\right|
\).
If #A = \matrix{2&3\\ 4 &5}#, then \(\det(A) = 2\cdot 5- 3\cdot 4 = -2.\)
If #A = \matrix{2&3\\ 4 &6}#, then \(\det(A) = 2\cdot 6- 3\cdot 4 = 0.\)
The term determinant of a square matrix can also be defined for matrices of larger size. We give the formal definition and a practical formula for \(3\times 3\) matrices, but pencil and paper calculations are in this course mostly \(2\times 2\) and \(3\times 3\) matrices.
For the definition of the determinant of an \(n\times n\) matrix we need the concept of permutation of \(n\) objects, in particular permutations of the numbers \(1, 2, \ldots, n\).
A permutation of the numbers \(1, 2, \ldots, n\) is just a rearrangement of these numbers. For example \(1\,2\) and \(2\,1\) are the two possible arrangements of the numbers \(1\) and \(2\). We denote the set of permutations of numbers \(1,\ldots,n\) as \(\mathcal{S}_n\) and we remark that the number of elements in this collection is equal to \(n!=1\times2\times\cdots\times n\).
All permutations of the numbers \(1,2,3\) are: \(\quad 1\,2\,3\quad 2\,3\,1\quad 3\,1\,2\quad 2\,1\,3\quad 1\,3\,2\quad\text{and}\quad 3\,2\,1\).
Let \(\sigma\) a permutation of the numbers \(1\ldots n\), say \(\sigma=j_1j_2\ldots j_n\). A misplaced pair in \(\sigma\) is a pair \((i,k)\) such that \(i<k\) and \(j_i>j_k\). We call a permutation \(\sigma\in \mathcal{S}_n\) odd or even if there is an even or odd number of misplaced pairs in \(\sigma\), respectively. We define the sign of \(\sigma\), denoted as\(\text{sgn}(\sigma)\), by \[\text{sgn}(\sigma)=\begin{cases} 1 & \text{if }\sigma\text{ is even}\\ -1& \text{if }\sigma\text{ is odd}\end{cases}\]
All even permutations of numbers \(1,2,3\) are: \(\phantom{x} 1\,2\,3\quad 2\,3\,1\quad\text{and}\quad 3\,1\,2\).
All odd permutations of numbers \(1,2,3\) are: \(\quad 2\,1\,3\quad 1\,3\,2\quad\text{and}\quad 3\,2\,1\).
For example, all misplaced pairs of the permutation \(2\,3\,1\) are the pairs \((1,3)\) and \((2,3)\). This is an even number.
Consider the permutation \(\sigma=3\, 4\, 1\, 5\, 7\, 6\, 2\) in \(\mathcal{S}_7\). The misplaced pairs of \(\sigma\) are \[(1,3), (1,7), (2,3), (2,7), (4,7), (5,6), (5,7), (6,7)\] The number of displaced pairs in \(\sigma\) is \(8\) and thus is \(\sigma\) even and \(\text{sgn}(\sigma)=1\).
Let \(A\) be an \(n\times n\) matrix: \[A=\matrix{a_{11} & \cdots & a_{1n}\\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn}}\] The determinant of \(A\), denoted as \(\textbf{det}(A)\) and also as \(\textbf{|}A\,\textbf{|}\), is the following sum which is summed over all permutations \(\sigma=j_1i_2\ldots j_n\) in \(\mathcal{S}_n\) : \[\text{det}(A) = \sum_{\sigma\in \mathcal{S}_n} \text{sgn}(\sigma)\,a_{1j_1}a_{2j_2}\cdots a_{nj_n}\]
Let \(A\) be an \(n\times n\) matrix are: \[A=\matrix{a_{11}&\cdots&a_{1n}\\ \vdots &\ddots&\vdots\\ a_{n1}&\cdots&a_{nn}}\] Then we write \(\text{det}(A)\) also as \[\left|\begin{array}{ccc}a_{11}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nn}\end{array}\right|\]
Take \(n=2\) and consider the matrix \[A=\matrix{a_{11} & a_{12}\\ a_{21} & a_{22}}\] There are now only two permutations of numbers \(1,2\). The two possible rearrangements of the numbers \(1\) and \(2\) are namely \(1\,2\) and \(2\,1\). The first has already the increasing order; the corresponding sign is thus \(1\) and the second permutation has a single misplaced pair, so that the sign thereof is equal to \(-1\). We get \[
\det(A) = \left|\,\begin{array}{rr}
a_{11} & a_{12}\\ a_{21} & a_{22}
\end{array}\,\right|=a_{11}\,a_{22} - a_{12}\,a_{21}\
\] which is consistent with the previous definition.
Take \(n=3\). Consider the determinant of the \(3\times3\) matrix \(A\) with \(i,j\)-element \(a_{ij}\) :
\[\det(A) =
\left|\,\begin{array}{rrr}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{array}\,\right|
\]
There are six permutations of the numbers \(1,2,3\). The permutations \(1\,2\,3\), \(2\,3\,1\) and \(3\,1\,2\) have sign \(1\), the other permutations \(2\,1\,3\), \(1\,3\,2\) and \(3\,2\,1\) have sign \(-1\). We get \[
\left|\,\begin{array}{rrr}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{array}\,\right|=\begin{array}{l l}
& a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32}\\
- & a_{11} a_{23} a_{32} - a_{12} a_{21} a_{33} - a_{13} a_{22} a_{31}
\end{array}
\] This expression is known as the rule of Sarrus. It is easy to remember. Place the first two columns behind the matrix
\[
\begin{array}{rrrrr}
a_{11} & a_{12} & a_{13} & a_{11} & a_{12}\\
a_{21} & a_{22} & a_{23} & a_{21} & a_{22}\\
a_{31} & a_{32} & a_{33} & a_{31} & a_{32}
\end{array}
\]
and now include the three terms on the main diagonal or parallel to it with a plus sign and the terms on the secondary diagonal or parallel to it with a minus sign.
The last expression for the determinant is a linear combination of three determinants of \(2\times 2\) submatrices, with alternating signs, obtained by deleting the first row and the column containing the coefficient. \[
\left|\,\begin{array}{rrr}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{array}\,\right|=a_{11}\cdot \left|\,\begin{array}{rrr}
a_{22} & a_{23}\\
a_{32} & a_{33}
\end{array}\,\right|
- a_{12}\cdot \left|\,\begin{array}{rrr}
a_{21} & a_{23}\\
a_{31} & a_{33}
\end{array}\,\right|+a_{13}\cdot \left|\,\begin{array}{rrr}
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{array}\,\right|\] Other expansions of the determinant in terms of \(2\times 2\) determinants are possible, as we will see.
For which exact value of #a# is the determinant of the following matrix #A# equal to #0#? \[ A = \matrix{1 & 3 & 5\\ 3 & 2 &2\\ 6& a& 4} \]
#a = # #4#
We first calculate the determinant of #A# :
\[ \begin{array}{rcl}\det(A)&=& a_{11}\cdot a_{22}\cdot a_{33} -a_{11}\cdot a_{23}\cdot a_{32} \\
&&-a_{12}\cdot a_{21}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31} \\
&&+a_{13}\cdot a_{21}\cdot a_{32}-a_{13}\cdot a_{22}\cdot a_{31} \\
&=& 1\cdot 2\cdot 4 -1\cdot 2\cdot a \\
&&-3\cdot 3\cdot 4+3\cdot 2\cdot 6 \\
&&5\cdot 3\cdot a-5\cdot 2\cdot 6 \\
&=&13\cdot a-52
\end{array} \]
The determinant is equal to #0# if and only if #a = 4#.
Consider two vectors \(\vec{u}=\cv{u_1\\u_2}\) and \(\vec{v}=\cv{v_1\\v_2}\) in \(\mathbb{R}^2\). If they are not multiples of each other, then they form together a parallelogram.
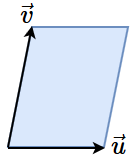
Then, the surface of this parallelogram is equal to the absolute value of \(\det\matrix{u_1 & v_1\\ u_2 & v_2}\).
Consider three vectors \(\vec{u}=\cv{u_1\\u_2\\u_3}\), \(\vec{v}=\cv{v_1\\v_2\\v_3}\), \(\vec{w}=\cv{w_1\\w_2\\w_3}\) in \(\mathbb{R}^3\) that do not all lie on a plane. Then, they together form a parallelopipedon.
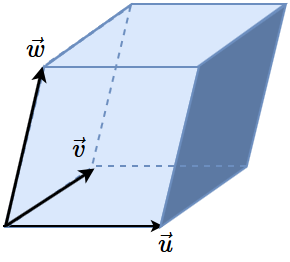
Then, the volume of the parallelopipedon is equal to \(\left|\det\!\!\matrix{u_1 & v_1 & w_1\\ u_2 & v_2 & w_3\\ u_3 & v_3 & w_3}\right|\).
 Determinant of a matrix
Determinant of a matrix




