Determinant van een matrix

Matrixrekening: Matrices

Determinant van een matrix

We hebben eerder in dit hoofdstuk gezien dat een $2\times 2$ -matrix $A=\matrix{a_{11} & a_{12}\\ a_{21} & a_{22}}$ inverteerbaar is als $a_{11}a_{22}-a_{12}a_{21}\neq 0$ . De uitdrukking $a_{11}a_{22}-a_{12}a_{21}$ noemen we de determinant van de matrix $A$ en noteren we als $\text{det}(A)$ .

De determinant van een ( $2\times 2$ )-matrix
$A=\left(\begin{array}{cc} a & b \\ c & d \end{array}\right)$
is het getal $a\cdot d-b\cdot c$ .

Gebruikelijke notaties voor de determinant van $A$ zijn $\det(A)$ en $\left|\begin{array}{cc} a & b \\ c & d \end{array}\right|$ .

Als $A = \matrix{2&3\\ 4 &5}$ , dan is $\det(A) = 2\cdot 5- 3\cdot 4 = -2.$

Als $A = \matrix{2&3\\ 4 &6}$ , dan is $\det(A) = 2\cdot 6- 3\cdot 4 = 0.$

Het begrip determinant van een vierkante matrix kun je ook voor matrices met grotere afmetingen definiëren. We geven de formele definitie en een concrete formule voor ( $3\times 3$ )-matrices, maar pen-en-papier berekeningen doen we in de cursus alleen maar voor $2\times 2$ en $3\times 3$ matrices.

Voor de definitie van de determinant van een ( $n\times n$ )-matrix hebben we het begrip permutatie van $n$ objecten nodig, in het bijzonder permutaties van de getallen $1, 2, \ldots, n$ .

Een permutatie van de getallen $1, 2, \ldots, n$ is niets meer en niets minder dan een rangschikking van deze getallen. Bijvoorbeeld $1\,2$ en $2\,1$ zijn de twee mogelijke rangschikkingen van de getallen $1$ en $2$ . We noteren de verzameling van permutaties van de getallen $1,\ldots,n$ als $\mathcal{S}_n$ en merken op dat het aantal elementen uit deze verzameling gelijk is aan $n!=1\times2\times\cdots\times n$ (spreek uit als $n$ faculteit).

Alle permutaties van de getallen $1,2,3$ zijn: $\quad 1\,2\,3\quad 2\,3\,1\quad 3\,1\,2\quad 2\,1\,3\quad 1\,3\,2\quad\text{en}\quad 3\,2\,1$ .

Laat $\sigma$ een permutatie van de getallen $1\ldots n$ zijn, zeg $\sigma=j_1j_2\ldots j_n$ . Een misplaatsing in $\sigma$ is een paar $(i,k)$ zodat $i<k$ en $j_i>j_k$ . We noemen een permutatie $\sigma\in S_n$ even of oneven als er een even respectievelijk oneven aantal misplaatsingen in $\sigma$ is. We definiëren het teken van $\sigma$ , genoteerd $\text{sgn}(\sigma)$ door $\text{sgn}(\sigma)=\begin{cases} 1 & \text{als }\sigma\text{ even is}\\ -1& \text{als }\sigma\text{ oneven is}\end{cases}$

Voorbeelden

Alle even permutaties van de getallen $1,2,3$ zijn: $\phantom{\text{on}}\quad 1\,2\,3\quad 2\,3\,1\quad\text{en}\quad 3\,1\,2$ .
Alle oneven permutaties van de getallen $1,2,3$ zijn: $\quad 2\,1\,3\quad 1\,3\,2\quad\text{en}\quad 3\,2\,1$ .
Bijvoorbeeld, alle misplaatsingen in de permutatie $2\,3\,1$ zijn de paren $(1,3)$ en $(2,3)$ . Dit is een even aantal.

Bekijk de permutatie $\sigma=3\, 4\, 1\, 5\, 7\, 6\, 2$ in $S_7$ . De misplaatsingen in $\sigma$ zijn $(1,3), (1,7), (2,3), (2,7), (4,7), (5,6), (5,7), (6,7)$ Het aantal misplaatsingen van $\sigma$ is $8$ , dus $\sigma$ is even en $\text{sgn}(\sigma)=1$ .

Laat $A$ een ( $n\times n$ )-matrix zijn: $A=\matrix{a_{11} & \cdots & a_{1n}\\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn}}$ De determinant van $A$ , genoteerd met $\textbf{det}(A)$ en ook met $\textbf{|}A\,\textbf{|}$ , is de volgende som, waarbij we sommeren over alle permutaties $\sigma=j_1i_2\ldots j_n$ in $\mathcal{S}_n$ : $\text{det}(A) = \sum_{\sigma\in \mathcal{S}_n} \text{sgn}(\sigma)\,a_{1j_1}a_{2j_2}\cdots a_{nj_n}$

Laat $A$ een ( $n\times n$ )-matrix zijn: $A=\matrix{a_{11}&\cdots&a_{1n}\\ \vdots &\ddots&\vdots\\ a_{n1}&\cdots&a_{nn}}$ Dan noteren we $\text{det}(A)$ ook als $\left|\begin{array}{ccc}a_{11}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nn}\end{array}\right|$

Neem $n=2$ en bekijk de matrix $A=\matrix{a_{11} & a_{12}\\ a_{21} & a_{22}}$ Er zijn nu slechts twee permutaties van de getallen $1,2$ . De twee mogelijke rangschikkingen van de getallen $1$ en $2$ zijn namelijk $1\,2$ en $2\,1$ . De eerste heeft al de goede volgorde; het bijbehorende teken is dus $1$ en de tweede heeft één misplaatsing, zodat het teken ervan gelijk is aan $-1$ . We vinden dus $\det(A) = \left|\,\begin{array}{rr} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\,\right|=a_{11}\,a_{22} - a_{12}\,a_{21}\$ in overeenstemming met de eerdere definitie.

Nu $n=3$ . Bekijk de determinant van de ( $3\times3$ )-matrix $A$ met $i,j$ -element $a_{ij}$ :
$\det(A) = \left|\,\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\,\right|$
Er zijn 6 permutaties van de getallen $1,2,3$ . De permutaties $1\,2\,3$ , $2\,3\,1$ en $3\,1\,2$ hebben het teken $1$ , de andere permutaties $2\,1\,3$ , $1\,3\,2$ en $3\,2\,1$ ) hebben teken $-1$ . We vinden $\left|\,\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\,\right|=\begin{array}{l l} & a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32}\\ - & a_{11} a_{23} a_{32} - a_{12} a_{21} a_{33} - a_{13} a_{22} a_{31} \end{array}$ Deze uitdrukking staat bekend als de regel van Sarrus. Hij is eenvoudig te onthouden. Zet de eerste twee kolommen achter de matrix
$\begin{array}{rrrrr} a_{11} & a_{12} & a_{13} & a_{11} & a_{12}\\ a_{21} & a_{22} & a_{23} & a_{21} & a_{22}\\ a_{31} & a_{32} & a_{33} & a_{31} & a_{32} \end{array}$
en neem nu de drie termen op de hoofddiagonaal of daar evenwijdig aan met een plusteken en de termen op de nevendiagonaal of daar evenwijdig aan met een minteken.

De laatste uitdrukking kun je ook schrijven als een lineaire combinatie van drie determinanten van $2\times 2$ deelmatrices, met alternerende tekens, verkregen door het schrappen van de eerste rij en de kolom die de coëfficiënt bevat. $\left|\,\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\,\right|=a_{11}\cdot \left|\,\begin{array}{rrr} a_{22} & a_{23}\\ a_{32} & a_{33} \end{array}\,\right| - a_{12}\cdot \left|\,\begin{array}{rrr} a_{21} & a_{23}\\ a_{31} & a_{33} \end{array}\,\right|+a_{13}\cdot \left|\,\begin{array}{rrr} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\,\right|$ Andere ontwikkelingen van de determinant in termen van $2\times 2$ determinanten zijn mogelijk, zoals we zullen zien

Voorbeeld

Voor welke exacte waarde van $a$ is de determinant van onderstaande matrix $A$ gelijk aan $0$ ? $A = \matrix{1 & 2 & -5\\ 3 & 7 &-2\\ 6& a& -4}$

$a =$ $14$

We berekenen eerst de determinant van $A$ :
$\begin{array}{rcl}\det(A)&=& a_{11}\cdot a_{22}\cdot a_{33} -a_{11}\cdot a_{23}\cdot a_{32} \\ &&-a_{12}\cdot a_{21}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31} \\ &&+a_{13}\cdot a_{21}\cdot a_{32}-a_{13}\cdot a_{22}\cdot a_{31} \\ &=& 1\cdot 7\cdot -4 -1\cdot -2\cdot a \\ &&-2\cdot 3\cdot -4+2\cdot -2\cdot 6 \\ &&-5\cdot 3\cdot a+5\cdot 7\cdot 6 \\ &=&182-13\cdot a \end{array}$
De determinant is dus dan en slechts dan gelijk aan $0$ als $a = 14$ .

Nieuw voorbeeld

Bekijk twee vectoren $\vec{u}=\cv{u_1\\u_2}$ en $\vec{v}=\cv{v_1\\v_2}$ in $\mathbb{R}^2$ . Als ze geen veelvoud van elkaar zijn, dan vormen ze samen een parallellogram.

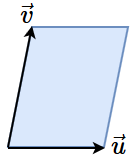
Dan is het oppervlak van dit parallellogram gelijk aan de absolute waarde van $\det\matrix{u_1 & v_1\\ u_2 & v_2}$ .

Bekijk drie vectoren $\vec{u}=\cv{u_1\\u_2\\u_3}$ , $\vec{v}=\cv{v_1\\v_2\\v_3}$ , $\vec{w}=\cv{w_1\\w_2\\w_3}$ in $\mathbb{R}^3$ die niet allemaal op een vlak liggen. Dan vormen ze samen een parallellepipedum.

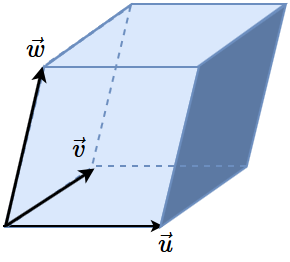
Dan is het volume van dit parallellepipedum gelijk aan $\left|\det\!\!\matrix{u_1 & v_1 & w_1\\ u_2 & v_2 & w_3\\ u_3 & v_3 & w_3}\right|$ .