Linear mappings: Introduction
 Introduction
Introduction
We have seen in the previous chapter how matrix-vector multiplication works. For any \(m\times n\) matrix \(A\) and for any vector \(\vec{x}\in\mathbb{R}^n\) the product \(A\vec{x}\in \mathbb{R}^m\) exists, when we consider the vector as an \(n\times 1\) matrix. In this way, a mapping of points in \(\mathbb{R}^n\) to (a subset of) points in \(\mathbb{R}^m\) is also defined. We say, in short: "\(A\) defines a mapping from \(\mathbb{R}^n\) into \(\mathbb{R}^m\)." We give two examples of matrix mappings. Such mappings "respect" the linear structure in the sense that linear combinations of vectors will be transformed into linear combinations of the image vectors. They are so-called linear mapping.
A model of human colour perception In the trichromatic theory of human colour perception, colour is in light-sensitive cells of the retina represented as activation of L, M and S cones, which are selectively sensitive to light of long, medium, and short wavelength, respectively (loosely related to 'red', 'green' and 'blue' light). The colours are not directly transmitted to the brain nerves, but in combinations. A classic model for processing LMS activations is called the theory of complementary colours and opponent processes of colour perception of Jameson and Hurvich. It is a model in which the signals of the L, M and S cones are re-coded in 3 channels with opponent processes. The "red-green" channel is responsible for the perception of red versus green (making that these colours can never be seen together, there is no such thing as a reddish green). The "red-green" channel activity (RG) is calculated by subtracting the activity of the M cones of the activity of the L cones and adding to the result the activity of the S-cones: \(RG = L-M+S\). The "yellow-blue" channel is responsible for the perception of yellow versus blue. The "yellow-blue" channel activity (YB) is calculated by adding the activity of the L cones and the M cones (the colour "yellow") and subtracting the activity of the S cones from this intermediate result: \(Y\!B = L+M-S\). In addition, there is still an achromatic luminance channel encoding black versus white. The achromatic brightness or luminance \(A\) can be calculated by the activities of all the cones together adding up: \(A=L+M+S\).
In summary:
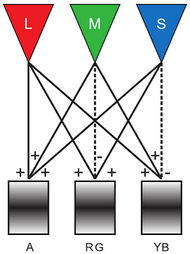 |
\[\left\{\begin{array}{rl} A &= L + M + S\\ RG &= L-M+S \\ Y\!B &= L+M-S\end{array}\right.\] |
In matrix notation we can write this as: \[\matrix{A\\ RG\\ Y\!B}=\matrix{1&1&1\\ 1&-1&1\\1&1&-1}\matrix{L\\ M\\ S}\] Thus, if we multiply the three-dimensional vector of cone activities with the above matrix, we get another three-dimensional vector of channel activity. Mathematically, we deal with a linear mapping of \(\mathbb{R}^3\) to \(\mathbb{R}^3\).
Reflection in the two-dimensional Euclidean space The matrix \(\matrix{0&1\\1&0}\) defines the linear mapping that maps the vector \(\cv{x\\y}\) in the Euclidean plane to \(\cv{y\\x}\). It is the reflection in the line \(y=x\).


