Lineaire afbeeldingen: Inleiding
 Inleiding
Inleiding
In het vorige hoofdstuk hebben we gezien hoe een matrix met een vector vermenigvuldigd wordt. Bij iedere \(m\times n\) matrix \(A\) en voor iedere vector \(\vec{x}\in\mathbb{R}^n\) bestaat het product \(A\vec{x}\in \mathbb{R}^m\). Daarmee is ook een afbeelding van punten in \(\mathbb{R}^n\) naar (een deelverzameling van) punten in \(\mathbb{R}^m\) gedefinieerd. We zeggen kortweg: "\(A\) definieert een afbeelding van \(\mathbb{R}^n\) naar \(\mathbb{R}^m\)." We geven twee voorbeelden van matrixafbeeldingen. Dergelijke afbeeldingen "respecteren" de lineaire structuur in de zin dat lineaire combinaties van vectoren in lineaire combinaties van de beeldvectoren worden overgevoerd. Het zijn zogenaamde lineaire afbeeldingen.
Een model voor kleurperceptie In lichtgevoelige cellen van de retina bij de mens wordt kleur gerepresenteerd door de activatie van L-, M- en S-kegeltjes, die selectief gevoelig zijn voor respectievelijk 'rood', 'groen', en 'blauw' licht. De kleuren worden niet direct, maar gecombineerd aan de hersenen doorgegeven. Een klassiek model voor het verwerken van de LMS-activaties is het zogeheten opponente processen model van Jameson en Hurvich voor het zien van kleuren. Het is een model waarin de signalen van de L-, M- en S-kegeltjes gehercodeerd worden in 3 kanalen met opponente processen. De letters L, M en S staan voor gevoeligheid voor lange, middellange en korte golflengtes van licht. Het 'rood-groen'-kanaal is verantwoordelijk voor de gewaarwording van rood versus groen (waardoor deze kleuren nooit samen gezien kunnen worden; er bestaat niet zoiets als roodachtig groen). De 'rood-groen'-kanaalactiviteit (RG) wordt berekend door de activiteit van de M-kegeltjes af te trekken van de activiteit van de L-kegeltjes en bij dit resultaat de activiteit van de S-kegeltjes op te tellen: \(RG = L-M+S\). Het 'geel-blauw'-kanaal is verantwoordelijk voor de gewaarwording van geel versus blauw. De 'geel-blauw'-kanaalactiviteit (YB) wordt berekend door de activiteit van de L-kegeltjes en de activiteit van de M-kegeltjes bij elkaar op te tellen (de kleur 'geel') en van dit tussenresultaat de activiteit van de S-kegeltjes af te trekken: \(Y\!B = L+M-S\). Daarnaast is er nog een achromatisch helderheidskanaal dat codeert voor zwart versus wit. De achromatische helderheid of luminantie \(A\) kan berekend worden door de activiteiten van alle kegeltjes bij elkaar op te tellen: \(A=L+M+S\).
Samengevat:
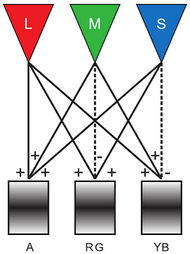 |
\[\left\{\begin{array}{rl} A &= L + M + S\\ RG &= L-M+S \\ Y\!B &= L+M-S\end{array}\right.\] |
In matrixnotatie kunnen we dit schrijven als: \[\matrix{A\\ RG\\ Y\!B}=\matrix{1&1&1\\ 1&-1&1\\1&1&-1}\matrix{L\\ M\\ S}\] Als we dus de 3-dimensionale vector van activiteiten van kegeltjes vermenigvuldigen met bovenstaande matrix, dan krijgen we een andere 3-dimensionale vector van kanaalactiviteiten. We hebben wiskundig te maken met een afbeelding van \(\mathbb{R}^3\) naar \(\mathbb{R}^3\).
Spiegeling in het platte vlak De matrix \(\matrix{0&1\\1&0}\) definieert de afbeelding die de vector \(\cv{x\\y}\) in het vlak afbeeldt op \(\cv{y\\x}\). Het is de spiegeling in de lijn \(y=x\).


