Lineaire afbeeldingen: Lineaire afbeeldingen
Kern en beeld van een matrixafbeelding
Voordat we de kern en het beeld van een lineaire afbeelding formeel invoeren bekijken we eerst een voorbeeld in de 3-dimensionale coördinaatruimte.
Beschouw de lineaire afbeelding \(L: \mathbb{R}^3\longrightarrow \mathbb{R}^3\) gedefinieerd door \[L\cv{x \\y\\z}=\cv{x-y-z\\ -x+y+z\\-x+y+z}\] Dit kunnen we als volgt herschrijven: \[L\cv{x \\y\\z}=x\cv{1\\-1\\-1}+y\cv{-1\\1\\1}+z\cv{-1\\1\\1}=(x-y-z)\cv{1\\-1\\-1}\] De verzameling van alle mogelijke beelden, het beeld van \(L\), is daarom de lijn \(\ell\) door de oorsprong met richtingsvector \(\cv{1\\-1\\-1}\). De volledige originelen van punten op deze lijn, dat wil zeggen alle punten in de ruimte die op een punt op de lijn \(\ell\) worden afgebeeld, zijn: \[\begin{aligned} L^{-1}\cv{a\\-a\\-a} &= \left\{\cv{x\\ y\\ z} \middle|\; x-y-z=a\right\} \\ \\ &= \left\{\cv{a+\lambda+\mu\\ \lambda\\ \mu} \middle|\; \lambda, \mu\in\mathbb{R}\right\} \\ \\ &= \cv{a\\ 0\\ 0}+ \lambda\cv{1\\1\\0}+\mu\cv{1\\0\\1}\end{aligned}\] Dit zijn parallelle vlakken (elk van die vlakken, die loodrecht op de richtingsvector van de lijn \(\ell\) staan, wordt afgebeeld op één punt).
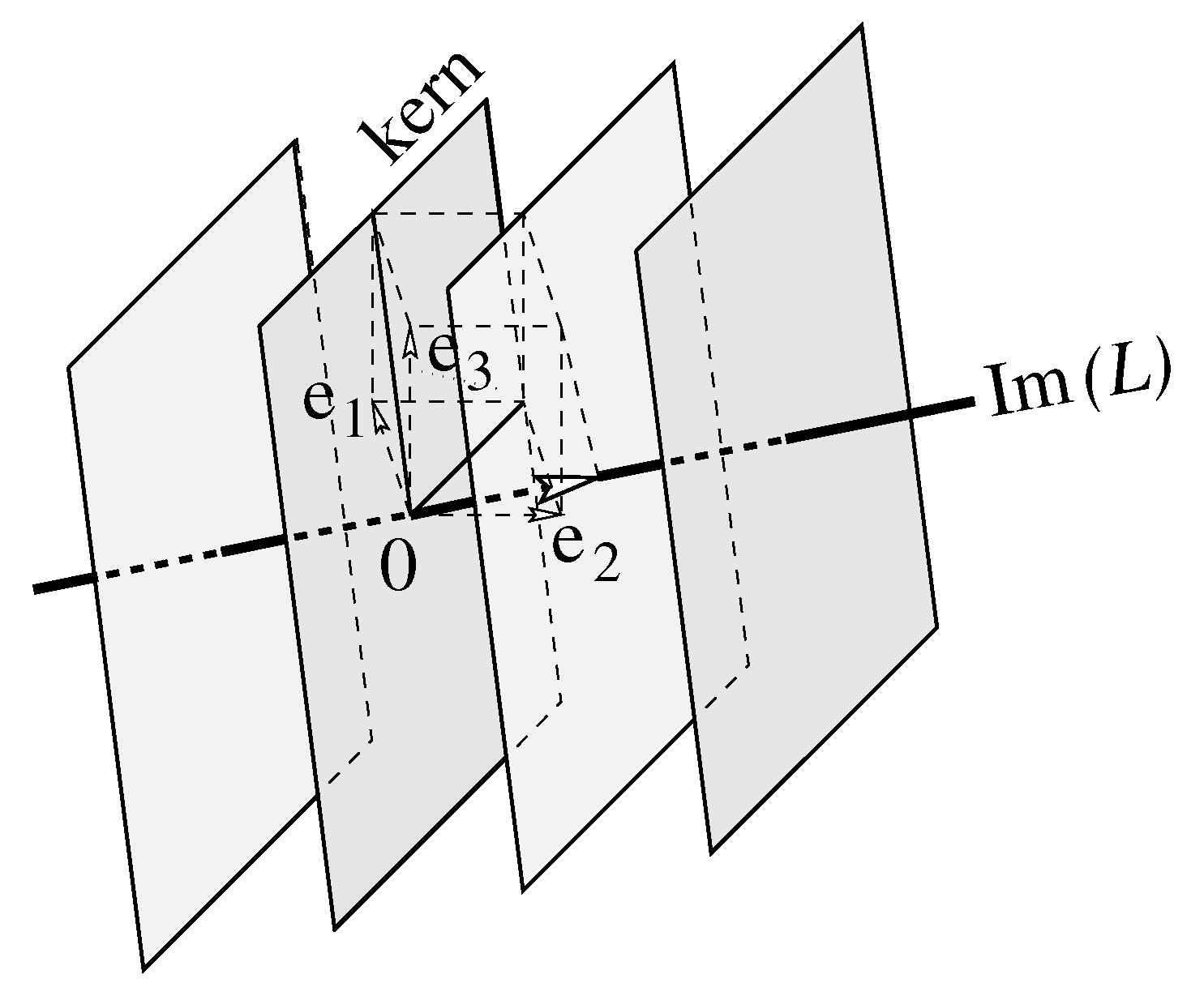
Slechts één van die vlakken gaat door de oorsprong, namelijk \(L^{-1}(\vec{0})\). Dit heeft de kern van \(L\).
Kern Laat \(A\) een \(m\times n\) matrix zijn en \(L_A: \mathbb{R}^n\longrightarrow \mathbb{R}^m\) de bijpassende matrixafbeelding zijn. De kern van \(L_A\), genoteerd met \(\text{ker}(L_A)\), is de verzameling vectoren \(\vec{v}\in \mathbb{R}^n\) die afgebeeld worden op de nulvector. In formuletaal: \[\text{ker}(L_A)=L_A^{-1}(\vec{0})=\{\vec{v}\in\mathbb{R}^n \mid L_A(\vec{v})=\vec{0}\}\]
Berekening van de kern De definitie van de kern van een matrixafbeelding \(L_A\) suggereert ook de methode om deze te berekenen: beschouw de matrix \(A\) als de coëfficiëntenmatrix van een homogeen stelsel lineaire vergelijkingen. Dan is de oplossingsverzameling van dit stelsel de kern van \(L_A\) en deze oplossingsverzameling vind je door middel van Gauss-eliminatie.
Beeld Laat \(A\) een \(m\times n\) matrix zijn en \(L_A: \mathbb{R}^n\longrightarrow \mathbb{R}^m\) de bijpassende matrixafbeelding zijn. Elke vector \(\vec{v}\in\mathbb{R}^n\) kun je schrijven als lineaire combinatie van de eenheidsvectoren \(\vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n\). Stel \[\vec{v}=\lambda_1 \vec{e}_1+ \lambda_2 \vec{e}_2+\cdots+\lambda_n \vec{e}_n\] dan is \[L_A(\vec{v})=\lambda_1 L_A(\vec{e}_1)+ \lambda_2 L_A(\vec{e}_2)+\cdots+\lambda_n L_A(\vec{e}_n)\] De verzameling van alle beelden van vectoren in \(\mathbb{R}^n\) onder de matrixafbeelding, dat wil zeggen, het beeld van \( L_A\), genoteerd als \(\text{im}(L_A)\), krijg je dus door het opspansel van de beelden van de eenheidsvectoren te bekijken. In formuletaal: \[\text{im}(L_A)=\sbspmatrix{L_A(\vec{e}_1),\ldots, L_A(\vec{e}_n)}\]
Berekening van het beeld De definitie van het beeld van een matrixafbeelding \(L_A\) suggereert ook de methode om deze te berekenen: je kunt het opspansel van de kolommen in de matrix \(A\) berekenen door rijreductie van de getransponeerde matrix \(A^{\top}\) tot trapvorm en de getransponeerde van dit tussenresultaat te nemen. De niet-nul kolommen van de op deze manier verkregen kolomvectoren spannen het beeld van \(L_A\) op.
\[\begin{aligned} \matrix{-9&15&6\\-6&10&4\\-3&5&2\\}&\sim\matrix{1&-{{5}\over{3}}&-{{2}\over{3}}\\-6&10&4\\-3&5&2\\}&{\blue{\begin{array}{c}-{{1}\over{9}}R_1\\\phantom{x}\\\phantom{x}\end{array}}}\\\\ &\sim\matrix{1&-{{5}\over{3}}&-{{2}\over{3}}\\0&0&0\\-3&5&2\\}&{\blue{\begin{array}{c}\phantom{x}\\R_2+6R_1\\\phantom{x}\end{array}}}\\\\ &\sim\matrix{1&-{{5}\over{3}}&-{{2}\over{3}}\\0&0&0\\0&0&0\\}&{\blue{\begin{array}{c}\phantom{x}\\\phantom{x}\\R_3+3R_1\end{array}}}\end{aligned}\] We krijgen een matrix met maar één niet-nulrij. Deze correspondeert met de vergelijking \[x-{{5\,y}\over{3}}-{{2\,z}\over{3}}=0\] Het is een vlak en is een 2-dimensionale ruimte. Dus: \[\text{ker}(L_A)\text{ is het vlak met vergelijking }x-{{5\,y}\over{3}}-{{2\,z}\over{3}}=0\text.\]
Om het beeld van \(L_A\) te bepalen bekijken we de getransponeeerde van \(A\) en berekenen de rijgereduceerde trapvorm hiervan. \[\begin{aligned} \matrix{-9&-6&-3\\15&10&5\\6&4&2\\}&\sim\matrix{1&{{2}\over{3}}&{{1}\over{3}}\\15&10&5\\6&4&2\\}&{\blue{\begin{array}{c}-{{1}\over{9}}R_1\\\phantom{x}\\\phantom{x}\end{array}}}\\\\ &\sim\matrix{1&{{2}\over{3}}&{{1}\over{3}}\\0&0&0\\6&4&2\\}&{\blue{\begin{array}{c}\phantom{x}\\R_2-15R_1\\\phantom{x}\end{array}}}\\\\ &\sim\matrix{1&{{2}\over{3}}&{{1}\over{3}}\\0&0&0\\0&0&0\\}&{\blue{\begin{array}{c}\phantom{x}\\\phantom{x}\\R_3-6R_1\end{array}}} \end{aligned}\] We krijgen in dit geval een matrix met maar één niet-nulrij. De getransponeerde hiervan is een kolomvector die het beeld van \(L_A\) opspant. Dus:\[ \text{im}(L_A)=\sbspmatrix{\matrix{1 \\ {{2}\over{3}} \\ {{1}\over{3}} \\ }}\]
Ter controle op correctheid van berekeningen van de kern en het beeld van een matrixafbeelding kun je checken of jouw antwoorden wel aan onderstaande dimensiestelling voldoen.
Dimensiestelling Beschouw een matrixafbeelding \(L_A\) van \(\mathbb{R}^n\) naar \(\mathbb{R}^m\) bepaald door de \(m\times n\) matrix \(A\). Introduceer de dimensie van de kern van \(L_A\) als het kleinste aantal vectoren dat de kern opspant; we noteren dit getal met \(\text{dim}\bigl(\text{ker}(L_A)\bigr)\) Evenzo definiëren we de dimensie van het beeld van \(L_A\), genoteerd as \(\text{dim}\bigl(\text{im}(L_A)\bigr)\), als het kleinste aantal opspannende vectoren van \(\text{im}(L_A)\). Dan geldt: \[\text{dim}\bigl(\text{im}(L_A)\bigr)+ \text{dim}\bigl(\text{ker}(L_A)\bigr)=n\]
