Transition to a different coordinate system

Linear mappings: Matrices and coordinate transformations

Transition to a different coordinate system

We will generalize the introductory example to the $n$ -dimensional Euclidean space $\mathbb{R}^n$ .

The unit vectors $\vec{e}_1=\cv{1\\0\\ \vdots \\ \vdots \\ 0}, \vec{e}_2=\cv{0\\1\\0\\ \vdots \\ 0} \ldots, \vec{e}_n=\cv{0\\ \vdots \\ \vdots \\ 0 \\ 1}$ belong to a choice of a coordinate system in the Euclidean space $\mathbb{E}^n$ . But you can also select a different coordinate system. In fact, you define then axis vectors $\vec{f}_{\!1}, \vec{f}_{\!2}, \ldots, \vec{f}_{\!n}$ along new axes. Let $\begin{aligned} \vec{f}_{\!1} &= c_{11}\vec{e}_1+c_{21}\vec{e}_2+\cdots + c_{n1}\vec{e}_n\\ \vec{f}_{\!2}&= c_{12}\vec{e}_1+c_{22}\vec{e}_2+\cdots + c_{n2}\vec{e}_n\\ &\;\;\vdots \\ \vec{f}_{\!n} &= c_{1n}\vec{e}_1+c_{2n}\vec{e}_2+\cdots + c_{nn}\vec{e}_n \end{aligned}$ Then the transformation matrix $[\textit{Id}]_e^f$ is defined by $[\textit{Id}\,]_e^f=\matrix{c_{11} & c_{12} & \cdots & c_{1n}\\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots\\ c_{n1} & c_{n2} & \cdots & c_{nn}}$ Make sure that you take the transformed form of the number scheme in the linear combinations of the $e$ vectors.

Each vector $\vec{v}$ in $\mathbb{E}^n$ can be written as linear combination $[\vec{v}]_e$ of the unit vectors $\vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n$ . We write $[\vec{v}]_e = \alpha_1\vec{e}_1+\alpha_2\vec{e}_2+\cdots + \alpha_n\vec{e}_n$ We can also do the $\vec{f}_{\!1}, \vec{f}_{\!2}, \ldots, \vec{f}_{\!n}$ : $[\vec{v}]_f = \beta_1\vec{f}_{\!1}+\beta_2\vec{f}_{\!2}+\cdots + \beta_n\vec{f}_{\!n}$ Naturally we ask ourselves what connection there is between the $\alpha$ -s and $\beta$ -s. Well:

$\cv{\alpha_1\\ \vdots \\ \alpha_n}= \matrix{c_{11} & \cdots & c_{1n}\\ \vdots & \ddots & \vdots \\ c_{n1} & \cdots & c_{nn}}\!\cv{\beta_1 \\ \vdots\\ \beta_n}$ In short notation: $[\vec{v}]_e = [\textit{Id}\,]_e^f\,[\vec{v}]_f$ The transformation matrix is be definition invertible and we denote this inverse by $[\textit{Id}\,]_f^e$ . In other words $[\vec{v}]_f = [\textit{Id}\,]_f^e\, [\vec{v}]_e = \left([\textit{Id}\,]_e^f\right)^{-1}[\vec{v}]_e$

Let $\vec{v}= \beta_1\vec{f}_{\!1}+\cdots + \beta_n\vec{f}_{\!n}$ and $\vec{v}= \alpha_1\vec{e}_{1}+\cdots + \alpha_n\vec{e}_{n}$ , then $[\vec{v}]_f =\cv{\beta_1 \\ \vdots\\ \beta_n}\quad\text{and}\quad [\vec{v}]_e\cv{\alpha_{\!1} \\ \vdots\\ \alpha_n}$ Because we can use the transformation matrix $[\textit{Id}\,]_e^f$ to write the $f$ -vectors as linear combinations of the $e$ -vectors, we have: $\begin{aligned} \vec{v} &=\beta_1\vec{f}_{\!1}+\cdots + \beta_n\vec{f}_{n} \\ \\ &= \quad \beta_1(c_{11}\vec{e}_{1}+c_{21}\vec{e}_{2}+\cdots c_{n1}\vec{e}_{n}) \\ &\quad{}+ \beta_2(c_{12}\vec{e}_{1}+c_{22}\vec{e}_{2}+\cdots c_{n2}\vec{e}_n)\\ &{} \quad {}\phantom{xxx}\vdots \\ &\quad {}+\beta_n(c_{1n}\vec{e}_1+c_{2n}\vec{e}_2+\cdots c_{nn}\vec{e}_{n}) \\ \\ &=\quad (\beta_1c_{11}+\beta_2 c_{12}+\cdots+\beta_n c_{1n})\vec{e}_{1} \\ &\quad{}+ (\beta_1 c_{21}+\beta_2 c_{22}+\cdots+\beta_n c_{2n})\vec{e}_{2}\\ &{} \quad {}\phantom{xxx}\vdots \\ &\quad{}+ (\beta_1c_{1n}+\beta_2 c_{2n}+\cdots+\beta_n c_{nn})\vec{e}_{n} \end{aligned}$ Dus: $\begin{aligned} \alpha_1 &= c_{11}\beta_1+ c_{12}\beta_2+\cdots+ c_{1n}\beta_n \\ \alpha_2 &= c_{21}\beta_1 + c_{22}\beta_2+\cdots+ c_{2n}\beta_n \\ &\vdots \\ \alpha_n &= c_{n1}\beta_1+ c_{n2}\beta_2+\cdots+ c_{nn}\beta_n\end{aligned}$ In matrixvector-vorm staat hier $\cv{\alpha_1\\ \vdots \\ \alpha_n}= \matrix{c_{11} & \cdots & c_{1n}\\ \vdots & \ddots & \vdots \\ c_{n1} & \cdots & c_{nn}}\!\cv{\beta_1 \\ \vdots\\ \beta_n}$

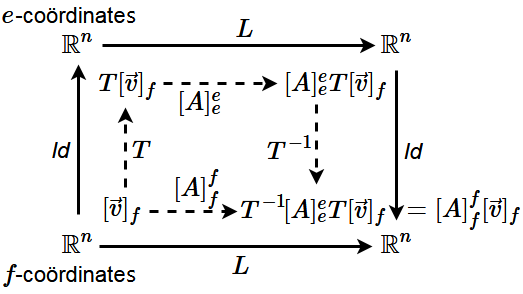
Let $L$ be a linear mapping from $\mathbb{R}^n$ to $\mathbb{R}^n$ . We already know that it is a matrix mapping when we choose of a coordinate system, that is, that there is a matrix $[A]_e^e$ such that $L(\vec{v}) = [A]_e^e\,[\vec{v}]_e$ . Here we have used the labels $e$ to indicate the selected coordinate system with corresponding unit vectors $\vec{e}_1,\ldots, \vec{e}_n$ . The same linear mapping $L$ can also be described with respect to another coordinate system with axis vectors $\vec{f}_{\!1},\ldots, \vec{f}_{\!n}$ by means of a matrix $[A]_f^f$ . The following theorem describes the relationship between the two matrices.

In the transition from $e$ -coordinates to $f$ -coordinates applies $[A]_f^f=[\textit{Id}\,]_f^e\cdot[A]_e^e\cdot[\textit{Id}\,]_e^f\tiny.$ If we abbreviate the transformation matrix $[\textit{Id}\,]_e^f$ , which describes the vectors $\vec{f}_{\!1}, \ldots \vec{f}_{\!n}$ as linear combinations of the vectors $\vec{e}_1, \ldots, \vec{e}_n$ , with the letter $T$ , we have $[A]_f^f=T^{-1}\cdot [A]_e^e\cdot T$ The diagram below illustrates the coordinate transformation.

For those wondering why we use the label $e$ twice in the matrix mapping $[A]_e^e$ : we do this so that we can also handle coordinate transformations in the case of a linear mapping from $\mathbb{R}^n$ to $\mathbb{R}^m$ . Suppose that we have chosen in the image space a coordinate system with unit vectors $\vec{f}_{\!1}, \ldots, \vec{f}_{\!m}$ , and suppose that we have chosen in the other space a coordinate system with unit vectors $\vec{e}_{1}, \ldots, \vec{e}_{n}$ , then a linear mapping $L$ with $\begin{aligned} L(\vec{e}_{\!1})=a_{11}\vec{f}_{\!1}+a_{12}\vec{f}_{\!2}+\cdots+a_{1m}\vec{f}_{\!m}\\ L(\vec{e}_{\!2})=a_{21}\vec{f}_{\!1}+a_{22}\vec{f}_{\!2}+\cdots+a_{2m}\vec{f}_{\!m}\\ &\vdots \\ L(\vec{e}_{\!n})=a_{n1}\vec{f}_{\!1}+a_{n2}\vec{f}_{\!2}+\cdots+a_{nm}\vec{f}_{\!m}\end{aligned}$ is a matrix mapping with $m\times n$ matrix $[A]_e^f=\matrix{a_{11} & \ldots & a_{n1}\\ \vdots & \ddots & \vdots\\ a_{1m} & \ldots & a_{nm}}$ such that each vector $\vec{v}$ is mapped on $L(\vec{v})$ via the matrix-vector multiplication $[L(\vec{v})]_f=[A]_e^f\,[\vec{v}]_e$

We can also choose different coordinate systems, such $e'$ - and $f'$ -coordinates instead $e$ - and $f$ -coordinates. Then: $\begin{aligned} {[A]}_{f'}^{e'} &=[\textit{Id}]_{f'}^{f}\cdot [A]_f^e\cdot [\textit{Id}]_e^{e'} \\ &=\left([\textit{Id}]_{f}^{f'}\right)^{-1}\cdot [A]_f^e\cdot [\textit{Id}]_e^{e'}\end{aligned}$ If we abbreviate the transformation matrix $[\textit{Id}\,]_e^{e'}$ that describes the vectors $\vec{e}_{1}', \ldots \vec{e}_{n}'$ as linear combinations of the vectors $\vec{e}_1, \ldots, \vec{e}_n$ , with the symbol $P$ , and if abbreviate the transformation matrix $[\textit{Id}\,]_{f}^{f'}$ that describes the vectors (\vec{f}'_{\!1}, \ldots \vec{f}'_{\!m}\) as linear combinations of the vectors $\vec{f}_{\!1}, \ldots \vec{f}_{\!n}$ , with the letter $Q$ , then we have: $[A]_{e'}^{f'}=Q^{-1}\cdot [A]_f^e\cdot P$

Let $L$ be the mapping from $\mathbb{R}^2$ to $\mathbb{R}^2$ defined by $L(x,y)=(2x+y, x-y)$
What is the matrix $[L]_e^e$ in terms of the unit vectors $\vec{e}_1=\cv{1\\0}$ and $\vec{e}_2=\cv{0\\1}$ ?

What is the matrix $[L]_f^f$ in $f$ -coordinates where $\vec{f}_{\!1}=\matrix{0 \\ 1 \\ }$ and $\vec{f}_{\!2}=\matrix{-1 \\ 2 \\ }$ ?

$[L]_e^e={}$ $\matrix{2 & 1\\ 1 & -1}$

$[L]_f^f={}$ $\matrix{1 & -3 \\ -1 & 0 \\ }$ .

The first equality follows from $L\cv{1\\ 0}=\cv{2\\1},\quad L\cv{0\\ 1}=\cv{1\\-1}$ by placing these image vectors as columns in the matrix.

The transformation matrix $T$ from $f$ -coordinates to $e$ -coordinates is given by $T=\matrix{0 & -1 \\ 1 & 2 \\ }\tiny.$ We also need the inverse of this transformation matrix. This can be calculated using the general formula for an inverse $2\times 2$ matrix, but perhaps better by the below row reduction process $\begin{aligned}\left(\begin{array}{rr|rr} 0&-1&1&0\\1&2&0&1\end{array}\right)&\sim\left(\begin{array}{rr|rr} 1&2&0&1\\0&-1&1&0\end{array}\right)&{\blue{\begin{array}{c}R_2\\R_1\end{array}}}\\\\ &\sim\left(\begin{array}{rr|rr} 1&2&0&1\\0&1&-1&0\end{array}\right)&{\blue{\begin{array}{c}\phantom{x}\\-R_2\end{array}}}\\\\ &\sim\left(\begin{array}{rr|rr} 1&0&2&1\\0&1&-1&0\end{array}\right)&{\blue{\begin{array}{c}R_1-2R_2\\\phantom{x}\end{array}}}\end{aligned}$ We read: $T^{-1} = \matrix{2 & 1 \\ -1 & 0 \\ }$
Then:
$\begin{aligned} {[L]}_f^f &=T^{-1}\cdot [L]_e^e \cdot T\\ \\ &= \matrix{2 & 1 \\ -1 & 0 \\ } \matrix{2 & 1\\ 1 & -1} \matrix{0 & -1 \\ 1 & 2 \\ } \\ \\ &= \matrix{5 & 1 \\ -2 & -1 \\ } \matrix{0 & -1 \\ 1 & 2 \\ }\\ \\ &=\matrix{1 & -3 \\ -1 & 0 \\ }\end{aligned}$

New example