Overgang op een ander coördinatenstelsel

Lineaire afbeeldingen: Matrices en coördinatentransformaties

Overgang op een ander coördinatenstelsel

We gaan het inleidende voorbeeld veralgemeniseren tot de $n$ -dimensionale Euclidische ruimte $\mathbb{R}^n$ .

De eenheidsvectoren $\vec{e}_1=\cv{1\\0\\ \vdots \\ \vdots \\ 0}, \vec{e}_2=\cv{0\\1\\0\\ \vdots \\ 0} \ldots, \vec{e}_n=\cv{0\\ \vdots \\ \vdots \\ 0 \\ 1}$ horen bij een keuze van een assenstelsel in de Euclidische ruimte $\mathbb{E}^n$ . Maar je kan ook een ander assenstelsel kiezen. In feite definieer je dan asvectoren $\vec{f}_{\!1}, \vec{f}_{\!2}, \ldots, \vec{f}_{\!n}$ langs nieuwe assen. Stel $\begin{aligned} \vec{f}_{\!1} &= c_{11}\vec{e}_1+c_{21}\vec{e}_2+\cdots + c_{n1}\vec{e}_n\\ \vec{f}_{\!2}&= c_{12}\vec{e}_1+c_{22}\vec{e}_2+\cdots + c_{n2}\vec{e}_n\\ &\vdots \\ \vec{f}_{\!n} &= c_{1n}\vec{e}_1+c_{2n}\vec{e}_2+\cdots + c_{nn}\vec{e}_n \end{aligned}$ Dan wordt de transformatiematrix $[\textit{Id}\,]_e^f$ gedefinieerd door $[\textit{Id}\,]_e^f=\matrix{c_{11} & c_{12} & \cdots & c_{1n}\\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots\\ c_{n1} & c_{n2} & \cdots & c_{nn}}$ Let op dat je de getransformeerde neemt van het getallenschema in de lineaire combinaties van de $e$ -vectoren.

Elke vector $\vec{v}$ in $\mathbb{E}^n$ kunnen we uitschrijven als lineaire combinatie $[\vec{v}]_e$ van de eenheidsvectoren $\vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n$ . We schrijven $[\vec{v}]_e = \alpha_1\vec{e}_1+\alpha_2\vec{e}_2+\cdots + \alpha_n\vec{e}_n$ Dat kunnen we ook doen met de $\vec{f}_{\!1}, \vec{f}_{\!2}, \ldots, \vec{f}_{\!n}$ : $[\vec{v}]_f = \beta_1\vec{f}_{\!1}+\beta_2\vec{f}_{\!2}+\cdots + \beta_n\vec{f}_{\!n}$ Natuurlijk vragen we ons af welke verband er tussen de $\alpha$ 's en de $\beta$ 's zijn. Welnu:

$\cv{\alpha_1\\ \vdots \\ \alpha_n}= \matrix{c_{11} & \cdots & c_{1n}\\ \vdots & \ddots & \vdots \\ c_{n1} & \cdots & c_{nn}}\!\cv{\beta_1 \\ \vdots\\ \beta_n}$ In korte notatie: $[\vec{v}]_e = [\textit{Id}\,]_e^f\,[\vec{v}]_f$ De transformatiematrix is per definitie inverteerbaar en we noteren deze inverse ook als $[\textit{Id}\,]_f^e$ . Met andere woorden $[\vec{v}]_f = [\textit{Id}\,]_f^e\, [\vec{v}]_e = \left([\textit{Id}\,]_e^f\right)^{-1}[\vec{v}]_e$

Stel $\vec{v}= \beta_1\vec{f}_{\!1}+\cdots + \beta_n\vec{f}_{\!n}$ en $\vec{v}= \alpha_1\vec{e}_{1}+\cdots + \alpha_n\vec{e}_{n}$ , dan $[\vec{v}]_f =\cv{\beta_1 \\ \vdots\\ \beta_n}\quad\text{en}\quad [\vec{v}]_e\cv{\alpha_{\!1} \\ \vdots\\ \alpha_n}$ Omdat we via de transformatiematrix $[\textit{Id}\,]_e^f$ de $f$ -vectoren als lineaire combinaties van de $e$ -vectoren kunnen schrijven, hebben we $\begin{aligned} \vec{v} &=\beta_1\vec{f}_{\!1}+\cdots + \beta_n\vec{f}_{n} \\ \\ &= \quad \beta_1(c_{11}\vec{e}_{1}+c_{21}\vec{e}_{2}+\cdots c_{n1}\vec{e}_{n}) \\ &\quad{}+ \beta_2(c_{12}\vec{e}_{1}+c_{22}\vec{e}_{2}+\cdots c_{n2}\vec{e}_n)\\ &{} \quad {}\phantom{xxx}\vdots \\ &\quad {}+\beta_n(c_{1n}\vec{e}_1+c_{2n}\vec{e}_2+\cdots c_{nn}\vec{e}_{n}) \\ \\ &=\quad (\beta_1c_{11}+\beta_2 c_{12}+\cdots+\beta_n c_{1n})\vec{e}_{1} \\ &\quad{}+ (\beta_1 c_{21}+\beta_2 c_{22}+\cdots+\beta_n c_{2n})\vec{e}_{2}\\ &{} \quad {}\phantom{xxx}\vdots \\ &\quad{}+ (\beta_1c_{1n}+\beta_2 c_{2n}+\cdots+\beta_n c_{nn})\vec{e}_{n} \end{aligned}$ Dus: $\begin{aligned} \alpha_1 &= c_{11}\beta_1+ c_{12}\beta_2+\cdots+ c_{1n}\beta_n \\ \alpha_2 &= c_{21}\beta_1 + c_{22}\beta_2+\cdots+ c_{2n}\beta_n \\ &\vdots \\ \alpha_n &= c_{n1}\beta_1+ c_{n2}\beta_2+\cdots+ c_{nn}\beta_n\end{aligned}$ In matrixvector-vorm staat hier $\cv{\alpha_1\\ \vdots \\ \alpha_n}= \matrix{c_{11} & \cdots & c_{1n}\\ \vdots & \ddots & \vdots \\ c_{n1} & \cdots & c_{nn}}\!\cv{\beta_1 \\ \vdots\\ \beta_n}$

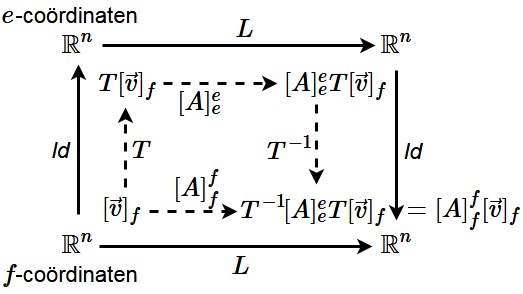
Stel dat $L$ een lineaire afbeelding van $\mathbb{R}^n$ naar $\mathbb{R}^n$ is. We weten al dat daar bij de keuze van een assenstelsel geldt dat het een matrixafbeelding is, dat wil zeggen, dat er een matrix $[A]_e^e$ bestaat zodanig dat $L(\vec{v}) = [A]_e^e\,[\vec{v}]_e$ . We hebben hier de labels $e$ gebruikt om aan te geven dat een assenstelsel is gekozen met bijpassende eenheidsvectoren $\vec{e}_1,\ldots, \vec{e}_n$ . Dezelfde lineaire afbeelding $L$ kan ook ten opzichte van een ander assenstelsel met asvectoren $\vec{f}_{\!1},\ldots, \vec{f}_{\!n}$ als matrixafbeelding beschreven worden, via een matrix $[A]_f^f$ . De volgende stelling beschrijft het verband tussen de twee matrices.

Bij overgang van $e$ -coördinaten naar $f$ -coördinaten geldt $[A]_f^f=[\textit{Id}\,]_f^e\cdot[A]_e^e\cdot[\textit{Id}\,]_e^f\tiny.$ Als we de transformatiematrix $[\textit{Id}\,]_e^f$ , die de vectoren $\vec{f}_{\!1}, \ldots \vec{f}_{\!n}$ beschrijft als lineaire combinaties van de vectoren $\vec{e}_1, \ldots, \vec{e}_n$ , afkorten met de letter $T$ , dan geldt dus $[A]_f^f=T^{-1}\cdot [A]_e^e\cdot T$ Onderstaand schema illustreert de coördinatentransformatie.

Voor wie zich afvraagt waarom we in de matrixafbeelding $[A]_e^e$ twee keer het label $e$ gebruiken: dit doen we om ook coördinatentransformaties te kunnen afhandelen in het geval van een lineaire afbeelding van $\mathbb{R}^n$ naar $\mathbb{R}^m$ . Stel dat we in de beeldruimte een assenstelsel met $\vec{f}_{\!1}, \ldots, \vec{f}_{\!m}$ als eenheidsvectoren gekozen hebben en dat we in de andere ruimte een assenstelsel met $\vec{e}_{1}, \ldots, \vec{e}_{n}$ als eenheidsvectoren gekozen hebben, dan wordt een lineaire afbeelding $L$ met $\begin{aligned} L(\vec{e}_{\!1})=a_{11}\vec{f}_{\!1}+a_{12}\vec{f}_{\!2}+\cdots+a_{1m}\vec{f}_{\!m}\\ L(\vec{e}_{\!2})=a_{21}\vec{f}_{\!1}+a_{22}\vec{f}_{\!2}+\cdots+a_{2m}\vec{f}_{\!m}\\ &\vdots \\ L(\vec{e}_{\!n})=a_{n1}\vec{f}_{\!1}+a_{n2}\vec{f}_{\!2}+\cdots+a_{nm}\vec{f}_{\!m}\end{aligned}$ een matrixafbeelding met ( $m\times n$ )-matrix $[A]_e^f=\matrix{a_{11} & \ldots & a_{n1}\\ \vdots & \ddots & \vdots\\ a_{1m} & \ldots & a_{nm}}$ zodanig dat elke vector $\vec{v}$ afgebeeld wordt op $L(\vec{v})$ via de matrix-vectorvermenigvuldiging $[L(\vec{v})]_f=[A]_f^e\,[\vec{v}]_e$

Ook kunnen we weer andere assenstelsels kiezen, bijvoorbeeld $e'$ - en $f'$ -coördinaten i.p.v. $e$ - en $f$ -coordinaten. Dan geldt: $\begin{aligned} {[A]}_{f'}^{e'} &=[\textit{Id}]_{f'}^{f}\cdot [A]_f^e\cdot [\textit{Id}]_e^{e'} \\ &=\left([\textit{Id}]_{f}^{f'}\right)^{-1}\cdot [A]_f^e\cdot [\textit{Id}]_e^{e'}\end{aligned}$ Als we de transformatiematrix $[\textit{Id}\,]_e^{e'}$ , die de vectoren $\vec{e}_{1}', \ldots \vec{e}_{n}'$ beschrijft als lineaire combinaties van de vectoren $\vec{e}_1, \ldots, \vec{e}_n$ , afkorten met de letter $P$ , en als we de transformatiematrix $[\textit{Id}]_{f}^{f'}$ , die de vectoren $\vec{f}'_{\!1}, \ldots \vec{f}'_{\!m}$ beschrijft als lineaire combinaties van de vectoren $\vec{f}_{\!1}, \ldots \vec{f}_{\!n}$ , afkorten met de letter $Q$ , dan geldt dus $[A]_{e'}^{f'}=Q^{-1}\cdot [A]_e^f\cdot P$

Laat $L$ de afbeelding van $\mathbb{R}^2$ naar $\mathbb{R}^2$ zijn gedefinieerd door $L(x,y)=(2x+y, x-y)$
Wat is de matrix $[L]_e^e$ t.o.v. eenheidsvectoren $\vec{e}_1=\cv{1\\0}$ en $\vec{e}_2=\cv{0\\1}$ ?

Wat is de matrix $[L]_f^f$ in $f$ -coördinaten waarbij $\vec{f}_{\!1}=\matrix{-1 \\ -3 \\ }$ en $\vec{f}_{\!2}=\matrix{1 \\ 4 \\ }$ ?

$[L]_e^e={}$ $\matrix{2 & 1\\ 1 & -1}$

$[L]_f^f={}$ $\matrix{22 & -27 \\ 17 & -21 \\ }$ .

De eerste gelijkheid volgt uit $L\cv{1\\ 0}=\cv{2\\1},\quad L\cv{0\\ 1}=\cv{1\\-1}$ door deze beeldvectoren als kolommen in de matrix te plaatsen.

De transformatiematrix $T$ van $f$ -coördinaten naar $e$ -coördinaten wordt gegeven door $T=\matrix{-1 & 1 \\ -3 & 4 \\ }\tiny.$ We hebben ook de inverse van deze transformatiematrix nodig. Deze kan berekend worden met de algemene formule voor inverse van een $(2\times 2$ )-matrix, maar misschien beter met onderstaand veegproces $\begin{aligned}\left(\begin{array}{rr|rr} -1&1&1&0\\-3&4&0&1\end{array}\right)&\sim\left(\begin{array}{rr|rr} 1&-1&-1&0\\-3&4&0&1\end{array}\right)&{\blue{\begin{array}{c}-R_1\\\phantom{x}\end{array}}}\\\\ &\sim\left(\begin{array}{rr|rr} 1&-1&-1&0\\0&1&-3&1\end{array}\right)&{\blue{\begin{array}{c}\phantom{x}\\R_2+3R_1\end{array}}}\\\\ &\sim\left(\begin{array}{rr|rr} 1&0&-4&1\\0&1&-3&1\end{array}\right)&{\blue{\begin{array}{c}R_1+R_2\\\phantom{x}\end{array}}}\end{aligned}$ We lezen af: $T^{-1} = \matrix{-4 & 1 \\ -3 & 1 \\ }$
Dan:
$\begin{aligned} {[L]}_f^f &=T^{-1}\cdot [L]_e^e \cdot T\\ \\ &= \matrix{-4 & 1 \\ -3 & 1 \\ } \matrix{2 & 1\\ 1 & -1} \matrix{-1 & 1 \\ -3 & 4 \\ } \\ \\ &= \matrix{-7 & -5 \\ -5 & -4 \\ } \matrix{-1 & 1 \\ -3 & 4 \\ }\\ \\ &=\matrix{22 & -27 \\ 17 & -21 \\ }\end{aligned}$

Nieuw voorbeeld