SVD, pseudoinverse, and PCA: SVD, pseudoinverse and PCA in R
 PCA
PCA
Let us carry out in R a principal component analysis in a concrete example.
We start with the creation of a data set of two quantities and its visualisation.
> N<-25
> X1 <- sort(rnorm(N)) # sort the first column
> X2 <- rep(2,N)+ 1.5*X1 + 0.25*rnorm(N) # data on a line + noise
> plot(X1, X2, type="p", col="blue", pch=1, asp=1)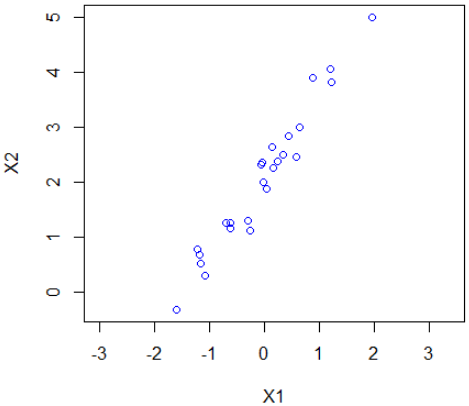
If we want to do a proper analysis, we first need to edit the data in such a way that the mean values of the two quantities are equal to zero.
> X1 <- X1-mean(X1)
> X2 <- X2-mean(X2)
> X <- cbind(X1,X2)From the data matrix \(X\) with two quantities (two columns) and \(N=25\) data (25 lines) we can construct the covariance matrix \(C\) as \[C = \frac{1}{N-1}X^{\top}\!X\] R has for this purpose the function cov on board.
> C <- 1/(N-1) * t(X) %*% X; C
X1 X2
X1 0.7483376 1.089108
X2 1.0891078 1.661375We now want to define new quantities whose values are uncorrelated. To do this, we diagonalise the covariance matrix by numerically solving the singular value decomposition of \(C\)
> svdC <- svd(C) # singular value decomposition of C
> V <- svdC$v; V
[,1] [,2]
[1,] -0.5538142 -0.8326403
[2,] -0.8326403 0.5538142
> S <- diag(svdC$d); S
[,1] [,2]
[1,] 2.385773 0.00000000
[2,] 0.000000 0.02393922
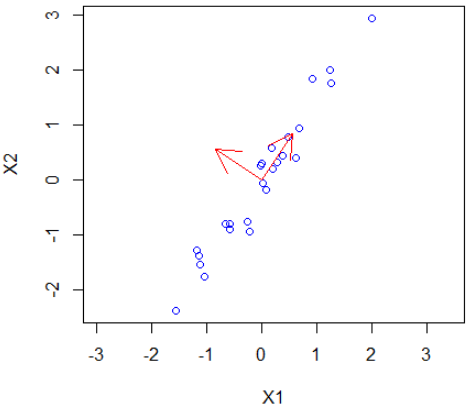
The eigenvectors define new quantities (as linear combinations of the old variables) that are uncorrelated since correlation is nothing else than dotproduct equal to zero for column vectors. In the figure below are shown the two vectors as part of a new coordinate system.
> plot(X1, X2, type="p", col="blue", pch=1, asp=1) > arrows(0, 0, -V[1,1], -V[2,1], col="red") > arrows(0, 0, V[2,1], V[2,2], col="red")
We can transform the data for the new coordinate system and visualise them. Because the eigenvalues are in increasing order, we have to switch columns during the computation.
> Y <- X %*% t(V); Y # transformed data
[,1] [,2]
[1,] 2.83855472 -0.02504232
[2,] 1.72813421 0.27607070
[3,] 1.77252406 0.18196905
[4,] 1.89608066 0.07139954
[5,] 2.04905404 -0.11153504
[6,] 1.03245369 0.10813638
[7,] 1.06534013 -0.01541172
[8,] 0.97677332 0.04009078
[9,] 0.78539110 -0.20678436
[10,] 0.89555155 -0.33257959
[11,] -0.20647606 0.14933024
[12,] -0.24741694 0.15946881
[13,] 0.03575947 -0.04127564
[14,] 0.09433655 -0.16633603
[15,] -0.59100438 0.17256342
[16,] -0.26799229 -0.05202771
[17,] -0.42391817 -0.05901045
[18,] -0.58422372 -0.07351742
[19,] -0.90964667 0.03826849
[20,] -0.66825077 -0.29052675
[21,] -1.15731713 -0.04643221
[22,] -2.04298603 0.24909232
[23,] -2.34162497 0.07674717
[24,] -2.16904238 -0.06608385
[25,] -3.56005399 -0.03657379
> Y1 <- Y[,1]
> Y2 <- Y[,2]
> plot(Y1, Y2, type="p", col="blue", pch=1, asp=1)
> arrows(0,0,1,0)
> arrows(0,0,0,1)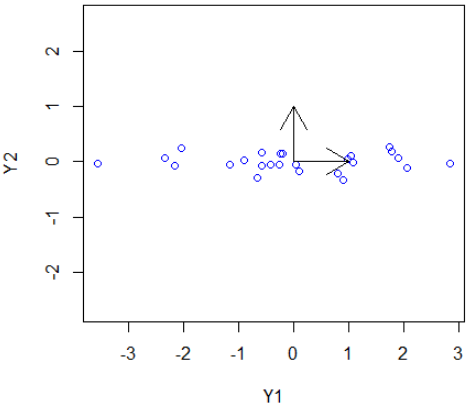
With the function var we can determine the variation in the quantities. One quantity then concerns \(99\%\) of the variation of the data, and the other quantity only \(1\%\).
> var(Y1)
[1] 2.385773
> var(Y2) [1] 0.02393922
varsY <- diag(var(Y)); varsY
[1] 2.38577326 0.02393922
> varsY/sum(varsY)
[1] 0.990065527 0.009934473\(\phantom{x}\)
We can of course also use the built-in function pca in R.
> pcaX <- prcomp(X, retx =TRUE, center=TRUE)
> summary(pcaX)
Importance of components:
PC1 PC2
Standard deviation 1.5446 0.15472
Proportion of Variance 0.9901 0.00993
Cumulative Proportion 0.9901 1.00000
> pcaX$rotation # coefficients of the principal components (factor loadings)
PC1 PC2
X1 0.5538142 0.8326403
X2 0.8326403 -0.5538142
> pcaX$x # transformed data
PC1 PC2
[1,] -2.83855472 0.02504232
[2,] -1.72813421 -0.27607070
[3,] -1.77252406 -0.18196905
[4,] -1.89608066 -0.07139954
[5,] -2.04905404 0.11153504
[6,] -1.03245369 -0.10813638
[7,] -1.06534013 0.01541172
[8,] -0.97677332 -0.04009078
[9,] -0.78539110 0.20678436
[10,] -0.89555155 0.33257959
[11,] 0.20647606 -0.14933024
[12,] 0.24741694 -0.15946881
[13,] -0.03575947 0.04127564
[14,] -0.09433655 0.16633603
[15,] 0.59100438 -0.17256342
[16,] 0.26799229 0.05202771
[17,] 0.42391817 0.05901045
[18,] 0.58422372 0.07351742
[19,] 0.90964667 -0.03826849
[20,] 0.66825077 0.29052675
[21,] 1.15731713 0.04643221
[22,] 2.04298603 -0.24909232
[23,] 2.34162497 -0.07674717
[24,] 2.16904238 0.06608385
[25,] 3.56005399 0.03657379
> round(sum(abs(Y + pcaX$x))) # in this example: Y = -pcaX$x
[1] 0