Laten we in een concreet voorbeeld de principale componenten analyse in R uitvoeren.
We beginnen met een dataset te creëren voor twee grootheden en de gegevens te visualiseren.

> N<-25
> X1 <- sort(rnorm(N))
> X2 <- rep(2,N)+ 1.5*X1 + 0.25*rnorm(N)
> plot(X1, X2, type="p", col="blue", pch=1, asp=1)

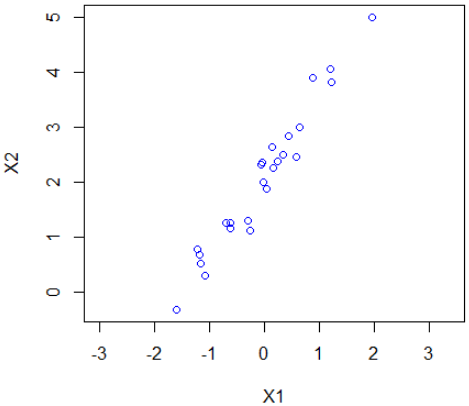
Om de analyse goed te kunnen uitvoeren moeten we de gegevens eerst bewerken zodanig dat de gemiddelde waarden van de twee grootheden gelijk aan nul zijn.

> X1 <- X1-mean(X1) 
> X2 <- X2-mean(X2)
> X <- cbind(X1,X2)

We kunnen voor de datamatrix \(X\) met 2 grootheden (2 kolommen) en \(N=25\) gegevens (25 rijen) dan de covariantiematrix \(C\) berekenen als \[C = \frac{1}{N-1}X^{\top}\!X\]

> C <- 1/(N-1) * t(X) %*% X; C
          X1       X2
X1 0.7483376 1.089108
X2 1.0891078 1.661375

We willen nu nieuwe grootheden definiëren wier waarden ongecorreleerd zijn. Hiervoor diagonaliseren we de covariantiematrix door het eigenwaardenprobleem voor de matrix \(C\) numeriek op te lossen. In dit voorbeeld gebruiken we daarentegen de singulierewaardenontbinding van \(C\) omdat deze beter aansluit bij de theorie waarin dimensiereductie centraal staat.

> svdC <- svd(C)   # singulierewaardenontbinding van C
> V <- svdC$v; V
           [,1]       [,2]
[1,] -0.5538142 -0.8326403
[2,] -0.8326403  0.5538142
> S <- diag(svdC$d); S
         [,1]       [,2]
[1,] 2.385773 0.00000000
[2,] 0.000000 0.02393922

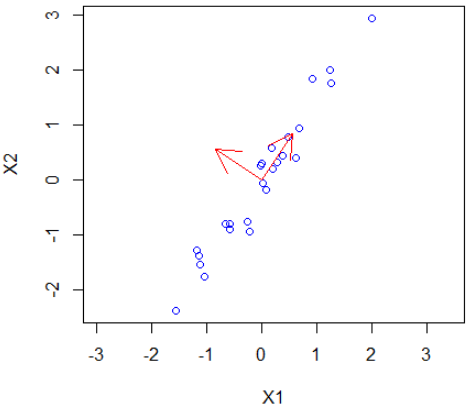
De eigenvectoren van \(C\) (gelijk aan de kolomvectoren van \(V\)) definiëren nieuwe grootheden (als lineaire combinaties van de oude grootheden) die ongecorreleerd zijn omdat correlatie niets ander is dan inproduct gelijk aan nul voor de kolomvectoren. In onderstaande figuur staan de twee vectoren afgebeeld als stukje van een nieuw coordinatensysteem.

> plot(X1, X2, type="p", col="blue", pch=1, asp=1)
> arrows(0, 0, -V[1,1], -V[2,1], col="red")
> arrows(0, 0,  V[2,1],  V[2,2], col="red")

We kunnen de gegevens transformeren voor het nieuwe coördinatensysteem en visualiseren. Omdat de eigenwaarden in opklimmende volgorde staan moeten we tussendoor kolommen verwisselen.

> Y <- X %*% t(V); Y   # getransfomeerde data
             [,1]        [,2]
 [1,]  2.83855472 -0.02504232
 [2,]  1.72813421  0.27607070
 [3,]  1.77252406  0.18196905
 [4,]  1.89608066  0.07139954
 [5,]  2.04905404 -0.11153504
 [6,]  1.03245369  0.10813638
 [7,]  1.06534013 -0.01541172
 [8,]  0.97677332  0.04009078
 [9,]  0.78539110 -0.20678436
[10,]  0.89555155 -0.33257959
[11,] -0.20647606  0.14933024
[12,] -0.24741694  0.15946881
[13,]  0.03575947 -0.04127564
[14,]  0.09433655 -0.16633603
[15,] -0.59100438  0.17256342
[16,] -0.26799229 -0.05202771
[17,] -0.42391817 -0.05901045
[18,] -0.58422372 -0.07351742
[19,] -0.90964667  0.03826849
[20,] -0.66825077 -0.29052675
[21,] -1.15731713 -0.04643221
[22,] -2.04298603  0.24909232
[23,] -2.34162497  0.07674717
[24,] -2.16904238 -0.06608385
[25,] -3.56005399 -0.03657379
> Y1 <- -Y[,1] # minteken vanwege tegengestelde van eerste eigenvector
> Y2 <-  Y[,2]
> plot(Y1, Y2, type="p", col="blue", pch=1, asp=1)
> arrows(0,0,1.25,0)
> arrows(0,0,0,1)

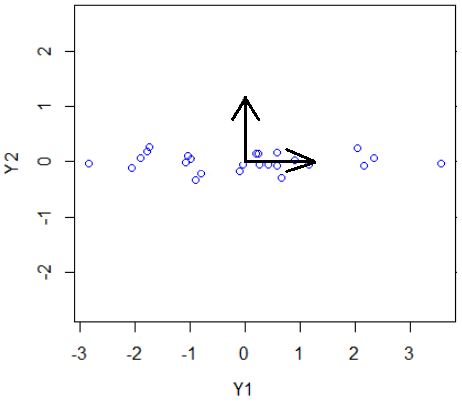
Met de functie var kunnen we de variatie in de grootheden bepalen. De ene grootheid betreft dan \(99\%\) van de variatie van de data, en de andere grootheid slechts voor \(1\%\).

> var(Y1)
[1] 2.385773
> var(Y2)
[1] 0.02393922
varsY <- diag(var(Y)); varsY
[1] 2.38577326 0.02393922
> varsY/sum(varsY)
[1] 0.990065527 0.009934473

\(\phantom{x}\)

We kunnen natuurlijk ook de ingebouwde functie pca in R gebruiken.

> pcaX <- prcomp(X, retx =TRUE, center=TRUE)
> summary(pcaX)
Importance of components:
                          PC1     PC2
Standard deviation     1.5446 0.15472
Proportion of Variance 0.9901 0.00993
Cumulative Proportion  0.9901 1.00000
> pcaX$rotation   # coëfficiënten van de principale componenten (factorladingen)
         PC1        PC2
X1 0.5538142  0.8326403
X2 0.8326403 -0.5538142
> pcaX$x        # getransformeerde data
              PC1         PC2
 [1,] -2.83855472  0.02504232
 [2,] -1.72813421 -0.27607070
 [3,] -1.77252406 -0.18196905
 [4,] -1.89608066 -0.07139954
 [5,] -2.04905404  0.11153504
 [6,] -1.03245369 -0.10813638
 [7,] -1.06534013  0.01541172
 [8,] -0.97677332 -0.04009078
 [9,] -0.78539110  0.20678436
[10,] -0.89555155  0.33257959
[11,]  0.20647606 -0.14933024
[12,]  0.24741694 -0.15946881
[13,] -0.03575947  0.04127564
[14,] -0.09433655  0.16633603
[15,]  0.59100438 -0.17256342
[16,]  0.26799229  0.05202771
[17,]  0.42391817  0.05901045
[18,]  0.58422372  0.07351742
[19,]  0.90964667 -0.03826849
[20,]  0.66825077  0.29052675
[21,]  1.15731713  0.04643221
[22,]  2.04298603 -0.24909232
[23,]  2.34162497 -0.07674717
[24,]  2.16904238  0.06608385
[25,]  3.56005399  0.03657379
> round(sum(abs(Y + pcaX$x)))  # in dit voorbeeld Y = -pcaX$x 
[1] 0