MATLAB heeft de functie svd aan boord om numeriek de singulierewaardenontbinding te bepalen. Met svds kun je de grootste 6 singuliere waarden berekenen (of andere gespecificeerde singuliere waarden). Eerst rekenen we het voorbeeld uit de lestekst na:

>> A = [2 0; 0 -3]
A =
     2     0
     0    -3
>> [U,S,V] = svd(A)  % matrices uit singulierewaardenontbinding
U =
     0     1
     1     0
S =
     3     0
     0     2
V =
     0     1
    -1     0
>> U*S*V' - A   % check
ans =
     0     0
     0     0
>> svds(A)      % grootste singuliere waarden
ans =
     3
     2

Het volgende voorbeeld van een singuliere matrix illustreert het verschil tussen exact en numeriek rekenen.

$$\begin{aligned}\matrix{1 & -1\\ -1 & 1} &= \matrix{-\frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2}}\matrix{2 & 0\\ 0 & 0}\matrix{-\frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2} & -\frac{1}{2}\sqrt{2}}\\ \\ &=\frac{1}{2}\sqrt{2} \matrix{-1 & 1\\ 1 & 1}\matrix{2 & 0\\ 0 & 0}\matrix{-1 & 1\\ -1 & -1}\frac{1}{2}\sqrt{2} \end{aligned}$$

>> B = [1 -1; -1 1]
B =
     1    -1
    -1     1
>> [U,S,V] = svd(B)    % singulierewaardendecompositie 
U =
   -0.7071    0.7071
    0.7071    0.7071
S =
    2.0000         0
         0    0.0000
V =
   -0.7071   -0.7071
    0.7071   -0.7071
>> U*S*V' - B          % check
ans =
   1.0e-15 *
   -0.3331    0.4441
         0   -0.2220
>> round(ans)          % afronden
ans =
     0     0
     0     0
>> svds(B)             % grootste singuliere waarden
ans =
2.0000
0.0000

Nu een voorbeeld van beeldcompressie aan de hand van een patroon bestaande uit witte en zwarte hokjes op een $9\times 9$ rooster. We specificeren de figuur met een matrix bestaande uit nullen (voor witte hokjes) en enen (voor zwarte hokjes):

$$M = \matrix{ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 1 & 1 &1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1\\ 0 & 1 & 0 & 1 & 1 &1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0}$$ In MATLAB kunnen we dit patroon visualiseren.

>> M = [
0 0 0 0 1 0 0 0 0;
0 0 0 1 0 1 0 0 0;
0 0 1 0 0 0 1 0 0;
0 1 0 1 1 1 0 1 0;
1 0 0 1 0 1 0 0 1;
0 1 0 1 1 1 0 1 0;
0 0 1 0 0 0 1 0 0;
0 0 0 1 0 1 0 0 0;
0 0 0 0 1 0 0 0 0];            % patroon
>> colormap([1 1 1; 0 0 0]);   % specificeer 2 kleuren: wit en zwart
>> image(M .* 255);            % patroon als zwart-wit figuur

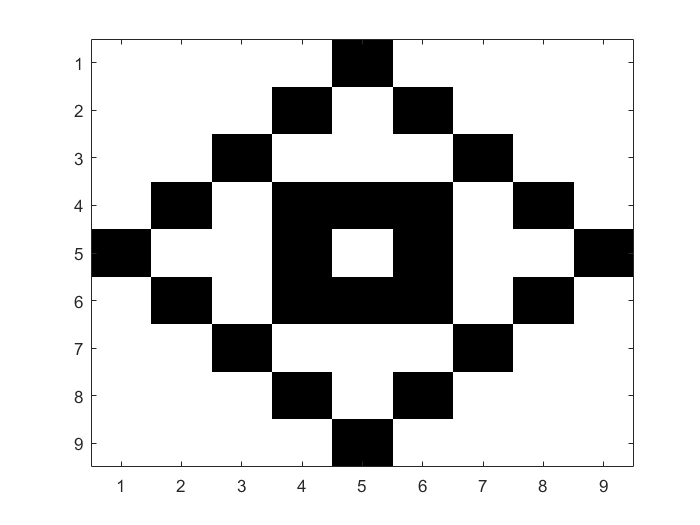
Stel nu dat we iemand dit patroon willen sturen. Dan kunnen we de matrix $M$ sturen, oftewel 81 getallen nul en één. Maar met de singulierewaardenontbinding kun je minder getallen sturen, terwijl het plaatje toch gereconstrueerd kan worden.

De eigenwaarden van de matrix $M$ zijn in stijgende volgorde als volgt:

>> sort(eig(M))
ans =
   -2.0000
   -0.9032
   -0.0000
   -0.0000
   -0.0000
    0.0000
    1.1939
    2.0000
    3.7093

Dus zijn de singuliere waarden van $M$ in dalende volgorde, afgerond op 1 decimaal, gelijk aan $3.7$, $2.0$, $1.2$, $0.9$ en $0$.

>> svds(M)
ans =
    3.7093
    2.0000
    2.0000
    1.1939
    0.9032
    0.0000

We benaderen $M$ nu met de eerste termen van de singulierewaardenontbinding. Maar in plaats van de numerieke waarden van de ontbinding te gebruiken voor beeldweergave ronden we matrixelementen af op gehele getallen $0$ en $1$ om het patroon te reconstrueren.

Stel dat we alleen de hoogste singuliere waarde $3.7$ gebruiken. Dan lijkt het plaatje al wat op de oorspronkelijke figuur:

>> [U,S,V] = svd(M);
>> M1 = round(U(:,1)*S(1,1)*V(:,1)'); 
>> image(M1 .* 255)

Hiervoor hoeven we dus maar $1+2\times 9 = 19$ numerieke waarden op te sturen, namelijk de singuliere waarde en de twee vectoren $\vec{u}_1$ en $\vec{v}_1$ .

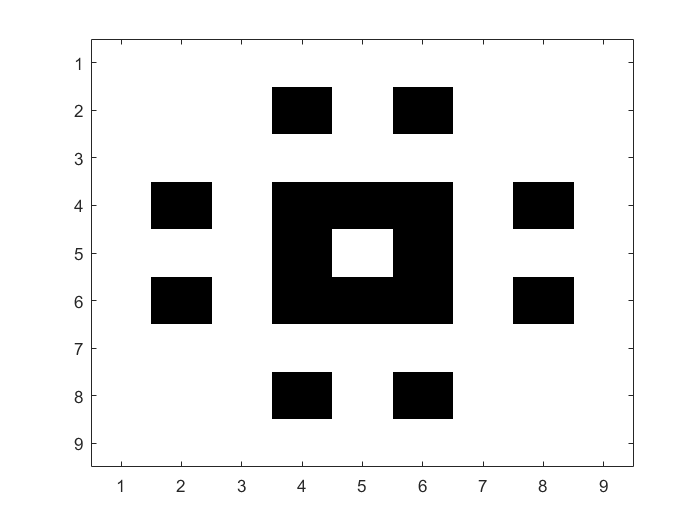
Als we ook de singuliere waarde $2$ gebruiken, dan krijgen we de oorspronkelijke figuur terug.

>> M3 = round(U(:,1:3)*S(1:3,1:3)*V(:,1:3)');
>> image(M3 .* 255)

Nu volstaat het opsturen van $3+6\times 9 = 57$ numerieke waarden, namelijk $3$ eigenwaarden en $2\times 3= 6$ vectoren. Dit lijkt niet zo veel minder dan $81$, het gaat toch al om een reductie van ongeveer $30\%$

$\phantom{xx}$

De winst is spectaculairder bij het sturen van grotere digitale beelden, bijvoorbeeld op de in computer vision veel gebruikte foto van $512\times 512$ pixels.

We lezen de foto in, berekenen de singulierewaardenontbinding van de bijpassende ($512\times 512$)-matrix met grijswaarden, en benaderen de originele foto met 8, 16, 32, 64, en 128 termen uit de ontbinding.

>> im = imread('E:/ANS/Lena512.bmp');
>> img = im2double(im);
>> size(img)
ans =
   512   512
>> imshow(img)
>> [U,S,V] = svd(img);
>> img8= U(:,1:8)*S(1:8,1:8)*V(:,1:8)';
>> imshow(img8)
>> img16= U(:,1:16)*S(1:16,1:16)*V(:,1:16)';
>> imshow(img16)
>> img32= U(:,1:32)*S(1:32,1:32)*V(:,1:32)';
>> imshow(img32)
>> img64= U(:,1:64)*S(1:64,1:64)*V(:,1:64)';
>> imshow(img64)
>> img128= U(:,1:128)*S(1:128,1:128)*V(:,1:128)';
>> imshow(img128)

Hieronder zie je de beelden voor verschillende waarden van het aantal termen $k$ die uit de singulierewaardenontbinding gehaald worden. Duidelijk is dat je minder informatie nodig hebt om toch een foto te hebben die op het zicht weinig afwijkt van het origineel (bij $k=64$ is de compressiefactor ongeveer $\frac{1}{4}$). Bij kleurenfoto's is de winst zelfs groter.

$k=8$	$k=16$
$k=32$	$k=64$
$k=128$	origineel: $k=512$