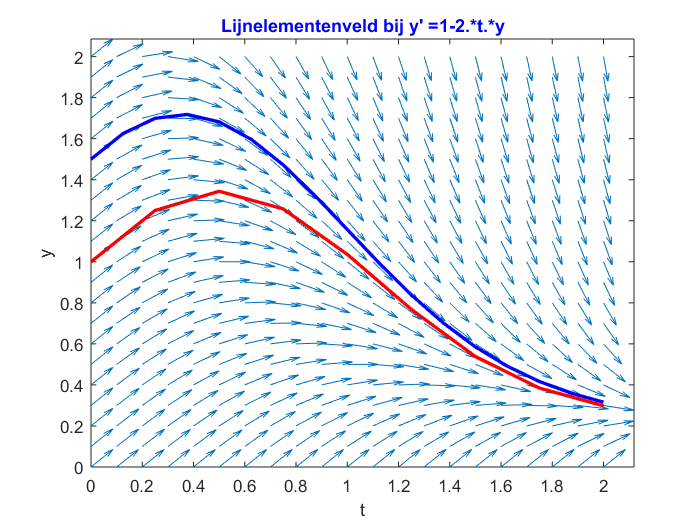
In onderstaande figuur zijn de via de voorwaartse Euler methode berekende functiewaarden voor het beginwaardeprobleem \(\frac{\dd y}{\dd t}=1-2t y,\; y(0)=1\) in een lijngrafiek te zien voor een stapgrootte \(dt=0.25\) (in de kleur rood). Om de kromme beter te kunnen interpreteren is het lijnelementenveld ook getekend in de figuur. Naarmate de stapgrootte \(dt\) kleiner is, wordt de grafiek van de berekende functiewaarden gladder en begint deze steeds meer op de grafiek van een exacte oplossing te lijken. Om dit te illustreren is de oplossingskromme voor het beginwaardeprobleem \(\frac{\dd y}{\dd t}=1-2t y,\; y(0)=1.5\) aan het diagram toegevoegd (in de kleur blauw met een stapgrootte van \(0.125\)).

MATLAB opdracht

Deel 1:

Maak een MATLAB programma dat de voorwaartse Euler methode implementeert voor een willekeurige functie \(\varphi(t,y)\) en pas deze dan eens toe op de volgende beginwaardeproblemen:

\[\frac{\dd y}{\dd t}=1-2ty,\qquad y(0)=1.5\]

\[\frac{\dd y}{\dd t}=1-2ty,\qquad y(0)=.25\]

\[\frac{\dd y}{\dd t}=y(1-\tfrac{1}{3}y),\qquad y(-1)=.25\]

\[\frac{\dd y}{\dd t}=y(1-\tfrac{1}{3}y),\qquad y(-1)=2.5\]

De belangrijkste functie in jouw programma noem je Euler en die heeft de volgende structuur

function [eta_data] = Euler(phi, t0, y0, t1, n)
    % phi: de functie bij de GDV dy/dt = phi(t,y)
    % t0:  tijd bij de beginwaarde y(t0) = y0 van de eerste oplossingskromme
    % y0:  beginwaarde van eerste oplossingskromme
    % t1:  eindtijd voor interval van de oplossingskrommen
    % n:   het aantal stappen in de Euler methode
    % OUTPUT: eta_data. Dit is een array van twee rijen. De eerste rij
    % bevat alle punten in de tijd en de tweede rij bevat alle berekende
    % functiewaarden.    

    ...

    end

Maak steeds een diagram waarin het lijnelementenveld en de grafiek van de oplossingskromme getekend zijn. Als de differentiaalvergelijking gelijk blijft, maar de beginwaarden wijzigen, dan kun je de oplossingskrommen in één figuur tekenen.

Deel 2:

Vergelijk de oplossingskromme van \[\frac{\dd y}{\dd t}=1-2\,t\,y,\qquad y(0)=1.5\] met verschillende waarden voor \(n\) met het resultaat van deze differentiaalvergelijking met behulp van een ODE solver in MATLAB (zoek maar eens op 'ode solver' in de help documentatie).