Deel 1:

Hieronder volgt een voorbeeld voor code die de voorwaartse Euler methode implementeert voor een willekeurige functie \(\varphi(t,y)\). Gekozen is om een Main functie te maken die de Euler functie aanroept, en waarin het plotten gebeurd. Dit kan natuurlijk ook andersom. Daarnaast is ervoor gekozen om apart op te kunnen geven wat de \(t\) en \(y\) ranges moeten zijn voor het tekenen van het lijnelementenveld. Verder kunnen extra beginwaarden en het bijbehorende gewenste aantal stappen aangegeven worden in twee arrays.

function [ output_args ] = VoorwaardseEulerMethode_Main( GDV, t0, y0, t1, n, 
draw_range_t, draw_range_y, y0_additional, n_additional)
% VoorwaardseEulerMethode_Main tekent het lijnelementenveld van de
% differentiaalvergelijking gespecificeerd als GDV en bepaald een
% oplossingskromme met startwaarde (t0,y0) met n stappen naar t1, via de 
% voorwaartse Euler methode.
% GDV: Als de differentiaalvergelijking van de vorm dy/dt = phi(t,y) is 
% dan moet GDV van de volgende vorm zijn: phi(t,y)
% t0: tijd bij de beginwaarde y(t0) = y0 van de eerste oplossingskromme
% y0: beginwaarde van eerste oplossingskromme
% t1: Eindtijd voor interval van de oplossingskrommen
% n: het aantal stappen in de Euler methode
% draw_range_t: het interval waarin het lijnelementenveld getekend moet
% worden. Van de vorm start_t : stap_t : eind_t.
% draw_range_y: het interval waarin het lijnelementenveld getekend moet
% worden. Van de vorm start_y : stap_y : eind_y.
% y0_additional: array met startwaarden voor extra oplossingskrommen in
% dezelfde figuur; van de vorm [y0_2,y0_3,y0_4,...].
% n_additional: array met bijbehorend aantal stappen voor de extra 
% oplossingskrommen; van de vorm [n_2,n_3,n_4,...].
% Bijvoorbeeld:
% VoorwaardseEulerMethode_Main('1-2.*t.*y',0,2,1,4,0:0.5:2,0:0.5:2,0.1,[],[])
% tekent het lijnelementenveld van de ODE 1-2ty vanaf t = 0 tot t = 2 met
% stappen van 0.5 en vanaf y = 0 tot y = 2 met stappen van 0.5. Voor de
% oplossingskromme is t0 = 0 en t1 = 1 waarbij n = 4. De startwaarde y0
% voor deze oplossingskromme is 2. De lengte van de lijnen is 0.1. Verder
% Zijn er geen extra oplossingskrommen die geplot moeten worden dus de
% laatste twee parameters zijn als lege arrays ingevuld.
% De waarden voor eta bij elke waarde voor t bepalen met de functie 'Euler':
eta_data = Euler(ODE , t0, y0, t1, n);

% Het lijnelementenveld tekenen en de oplossingskromme erin. Hieronder is
% de MATLAB functie quiver gebruikt maar je kunt ook je eerder gemaakte
% functie gebruiken die de lijnen tekent
[t,y] = meshgrid(draw_range_t,draw_range_y);
helling = eval(ODE);
hoek = atan(helling);
dt = cos(hoek); % bij eigen functie die lijnen tekent hier lengte_lijnen*cos(hoek) nodig.
dy = sin(hoek); % bij eigen functie die lijnen tekent hier lengte_lijnen*sin(hoek) nodig.
figure('Color','White')

% Kleur en lijntype instellen (het lijnelementveld wordt als eerste object gezien):
set(0,'defaultAxesColorOrder',[1 0 0;0 0 1;1 0 1;0 1 0],
'defaultAxesLineStyleOrder','-|-|--|:') 

% Het lijnelementveld tekenen. De kleur handmatig instellen omdat het veld als eerste 
% object wordt gezien voor de kleuren en lijnstijlen hierboven gespecificeerd.
quiver(t,y,dt,dy,'Color',[0 114/255 190/255]) 

hold all % later toegevoegde grafieken doen mee met de rotatie in kleur en lijntype. 

% De eerste oplossingskromme tekenen. De kleur handmatig instellen omdat het veld 
% als eerste object wordt gezien en de oplossingskromme anders blauw wordt. 
plot(eta_data(1,:),eta_data(2,:),'r','LineWidth',2) 

title(strcat('Lijnelementenveld bij y',char(39),' = ',ODE),'Color','Blue')
xlabel('t')
ylabel('y')
box on
set(gcf,'Color','White')
axis tight

% Voor meerdere oplossingskrommen:
aantal_extra_startwaarden = length(y0_additional);
if aantal_extra_startwaarden == 0
    return
else    
    for nr = 1:aantal_extra_startwaarden
        y0_nr = y0_additional(nr);
        n_nr = n_additional(nr);
        eta_data_extra = Euler(GDV , t0, y0_nr, t1, n_nr);        
        plot(eta_data_extra(1,:),eta_data_extra(2,:),'LineWidth',2)

    end
end
end

function [eta_data] = Euler(phi, t0, y0, t1, n)
    % phi: de functie bij de GDV dy/dt = phi(t,y)
    % t0: tijd bij de beginwaarde y(t0) = y0 van de eerste oplossingskromme
    % y0: beginwaarde van eerste oplossingskromme
    % t1: Eindtijd voor interval van de oplossingskrommen
    % n: het aantal stappen in de EUler metode
    % Output: eta_data. Dit is een array van twee rijen. De eerste rij bevat
    % alle punten in de tijd en de tweede rij bevat alle berekende functiewaarden.
    
    % Stapgrootte bepalen en de array met waarden voor t:
    dt = (t1 - t0) / n ;
    calc_range_t = t0:dt:t1;

    % Een matrix initialiseren en vullen met de functiewaarden
    eta_prev = y0; % De eerste waarde die voor eta_prev gebruikt moet worden.
    eta_data = zeros(2,length(calc_range_t)); % De data matrix alvast vullen met nullen.
    eta_data(1,1) = t0; % t0 is nu opgeslagen in het element met index 1.
    eta_data(2,1) = y0; % y0 is nu opgeslagen in het element met index 1.
    for k = 2:n+1 % y0,y1,y2, ... zitten in de array met respectievelijk index 1,2,3,...
                  % omdat we y0 al hebben starten we bij k = 2.
        t = calc_range_t(k-1); % Waarde voor t_{k-1}. Deze wordt gebruikt in eval(phi).
        y = eta_data(2,k-1); % Waarde voor eta_{k-1}. Deze wordt gebruikt in eval(phi).
        eta_data(1,k) = calc_range_t(k);
        eta_data(2,k) = eta_prev + eval(phi)*dt;
        eta_prev = eta_data(2,k); 
    % Huidige berekende waarde opslaan om bij de volgende stap weer te kunnen gebruiken.
    end   
end

Het commando

>> VoorwaardseEulerMethode_Main('1-2.*t.*y',0,1,2,8,0:0.1:2,0:0.1:2,[1.5],[16])

resulteert in de grafiek die we bij de opdracht als voorbeeld gaven:

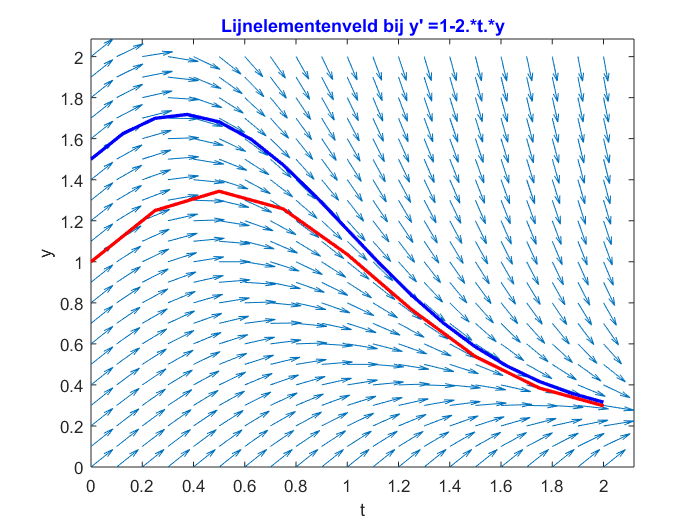
Voor het samen plotten van \[\frac{\dd y}{\dd t}=1-2ty,\qquad y(0)=1.5\] en \[\frac{\dd y}{\dd t}=1-2ty,\qquad y(0)=.25\] voeren we het volgende commando uit:

>> VoorwaardseEulerMethode_Main('1-2.*t.*y',0,1.5,2,32,0:0.1:2,0:0.1:2,[0.25],[32])

Dit resulteert in:

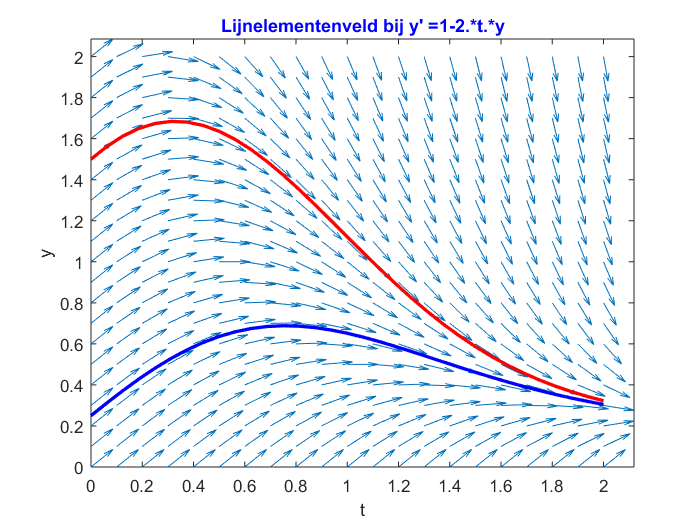
Voor het samen plotten van \[\frac{\dd y}{\dd t}=y(1-\tfrac{1}{3}y),\qquad y(-1)=.25\] en \[\frac{\dd y}{\dd t}=y(1-\tfrac{1}{3}y),\qquad y(-1)=2.5\] voeren we het volgende commando uit:

>> VoorwaardseEulerMethode_Main('y.*(1-(1/3)*y)',0,0.25,4,32,0:0.2:4,0:0.2:4,[2.5],[32])

Dit resulteert in:

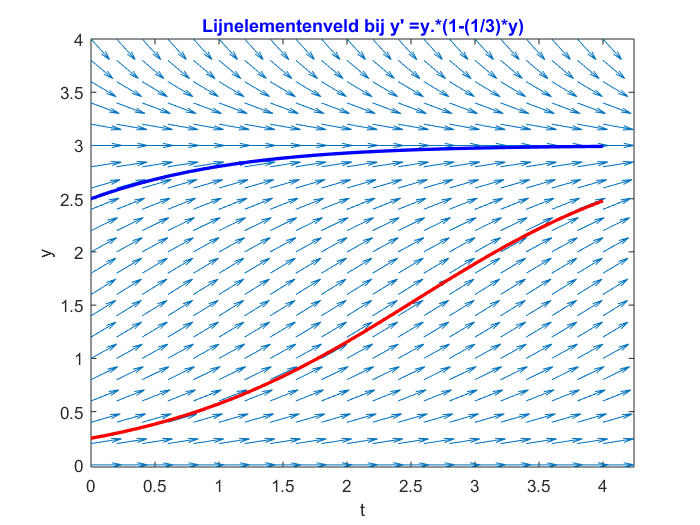
Nu kunnen we ook heel makkelijk variëren in startwaarden en de waarde voor \(n\). Hieronder staan voor de differentiaalvergelijking \[\frac{\dd y}{\dd t}=1-2ty\] verschillende oplossingskrommen geplot met startwaarden \(0.5\), \(1\), \(1.5\) en \(2\). De bijbehorende gebruikte waarden voor \(n\) zijn respectievelijk \(4\), \(8\), \(16\) en \(32\). Hiervoor is het volgende commando gebruikt:

>> VoorwaardseEulerMethode_Main('y.*(1-2.*t.*y)',0,0.5,2.5,4,0:0.1:2.5,0:0.1:2.5,[1,1.5,2],[8,16,32])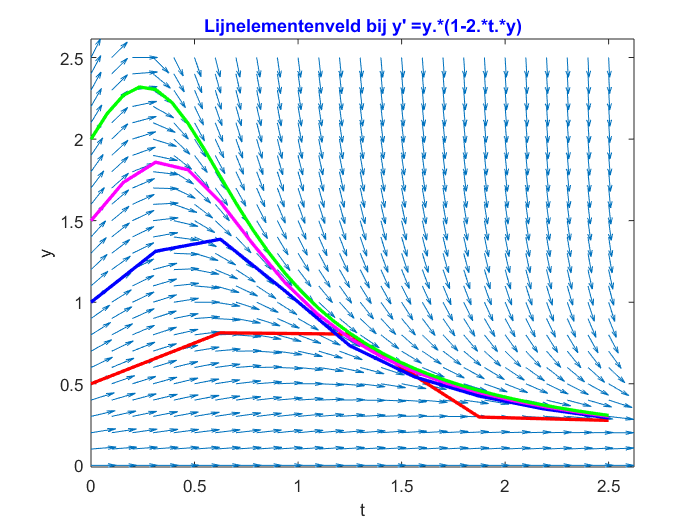

Deel 2

Voor het tweede deel gebruiken we de bovenstaande functie om de oplossingskromme bij een bepaalde startwaarde met verschillende waarden voor \(n\) te plotten in dezelfde figuur. Daarna voegen we in het command window het resultaat toe van een 'ode solver'. Een geschikte ode solver is ode45.

De commando's die je uitvoert zouden er zo uit kunnen zien:

>> VoorwaardseEulerMethode_Main('1-2.*t.*y',0,1.5,2,4,0:0.1:2,0:0.1:2,[1.5,1.5,1.5,1.5],[8,16,32,64])
>> [t,y] = ode45(@(t,y) 1-2*t*y,[0,2],1.5);
>> plot(t,y,'k-','LineWidth',2)
>> legend('','n = 4','n = 8','n = 16','n = 32','n = 64','ODE solver')
>> set(0,'defaultAxesColorOrder','remove','defaultAxesLineStyleOrder','remove')

Dit resulteert in:

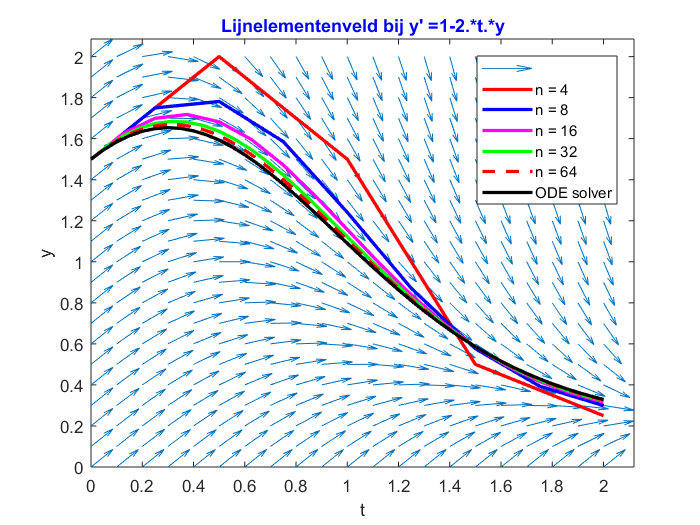
We zien dus dat, naarmate \(n\) groter wordt, het resultaat van de voorwaardse Euler methode steeds dichter bij de oplossing gegeven door de ode solver komt te liggen.