ODE of order 1 We consider the differential equation $$\frac{\dd y}{\dd t}=1-2\,t\,y$$ and calculate numerically solution curves for initial values $y(0)=0.5$, $y(0)=1$, and $y(0)=1.5$. We draw the solution curves with a slope field in the background.

First, we create an M file, ode1.m, with the following contents.

function dydt = ode1(t,y)
% compute dydt = 1 - 2*t*y
    dydt = 1 - 2*t.*y;
end

The only thing that this script does is to use values $t$ and $y$ to compute the derivative $\frac{\dd y}{\dd t}$ at the point $(t,y)$. Hereafter, for a given time domain and several initial values, we can numerically solve the corresponding initial value problem.

>> clear
>> options = odeset('RelTol', 1e-5); % set accuracy
>> tdomain = [0,2];
>> y0 = [0.5, 1.0, 1.5];  % initial values
>> [t,y] = ode45('ode1', tdomain, y0, options);
>> % graphs of solutions can be drawn
>> plot(t, y(:,1), '-b', t, y(:,2), '-g', t, y(:,3), '-k', 'LineWidth', 3);
>> hold on
>> % add a slope field
>> [t,y] = meshgrid(0:0.1:2, 0:0.1:2);
>> dy = 1 - 2*t.*y;
>> dt = ones(size(dy));
>> L = sqrt(dt.^2 + dy.^2);
>> dyu = dy./L;
>> dtu = dt./L;
>> quiver(t, y, dtu, dyu, 0.5, 'r'), axis tight
>> xlabel 't', ylabel 'y';
>> title("Lijnelementenveld en oplossingskrommen bij y' = 1 - 2ty",'Color','Red')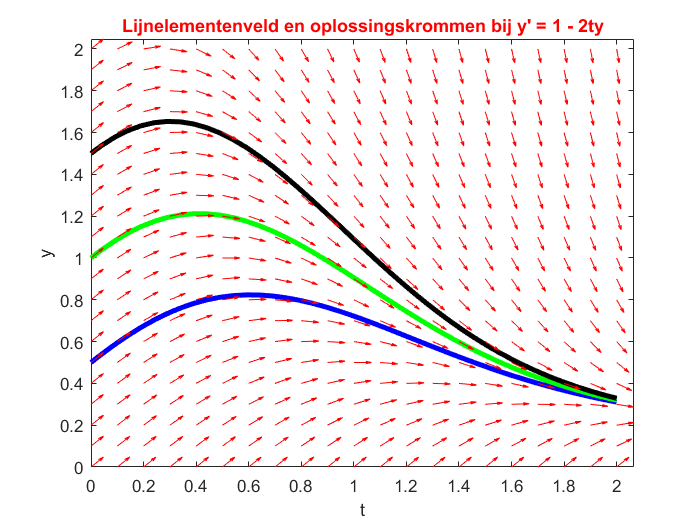

Van der Pol equation As an example of numerically solving an ODE of order 2 we consider the van der Pol equation $$\frac{\dd^2y}{\dd t^2} -\frac{1}{\varepsilon}(1-y^2)\frac{\dd y}{\dd t}+y = 0$$ with $0<\varepsilon\ll 1$. As an example, let's take the fairly large value of $\varepsilon=\tfrac{1}{2}$ to show more clearly what is happening. We calculate numerically the solutions at initial values $y(0)=0, y'(0)=-1$ and at $y(0)=3, y'(0)=-1$.

Because the numerical solution method ode45 only works for ordinary differential equations of order 1 or systems of 1st order differential equations, we first rewrite the van der Pol equation as a system of two coupled 1st order differential equations. Introduce $$y_1=y, y_2 = \frac{\dd y}{\dd t}$$ then $$\frac{\dd y_2}{\dd t} = \frac{\dd^2y}{\dd t^2} = \frac{1}{\varepsilon}(1-y_1^2)\,y_2-y_1$$ In short, the van der Pol equation corresponds with the following system of 1st order differential equations $$\left\{\begin{aligned} \dfrac{\dd y_1}{\dd t} &= y_2\\ \dfrac{\dd y_2}{\dd t} &= \frac{1}{\varepsilon}(1-y_1^2)\,y_2-y_1 \end{aligned}\right.$$ First, we therefore create an M-file, ode2.m, with the following contents.

function dydt = gdv2(t,y)
% van der Pol equation with epsilon = 1/2
    dydt = [y(2); 2*(1-y(1)^2)*y(2)-y(1)];
end

Hereafter, for a given time domain and several initial values, we can numerically solve the corresponding initial value problem. The diagram below is obtained by the following code.

>> clear
>> options = odeset('RelTol', 1e-5); % set accuraccy
>> tdomain = [0,30];
>> figure
>> y0 = [0,-1];  % firis initial values
>> [t,y] = ode45('ode2', tdomain, y0, options);
>> plot(t,y(:,1),'-b')
>> hold on
>> y0 = [3,-1];  % second initial values
>> [t,y] = ode45('ode2', tdomain, y0, options);
>> plot(t,y(:,1),'-r')
>> xlabel 't', ylabel 'y';
>> title("Oplossingskrommen bij van der Pol vergelijking",'Color','Red')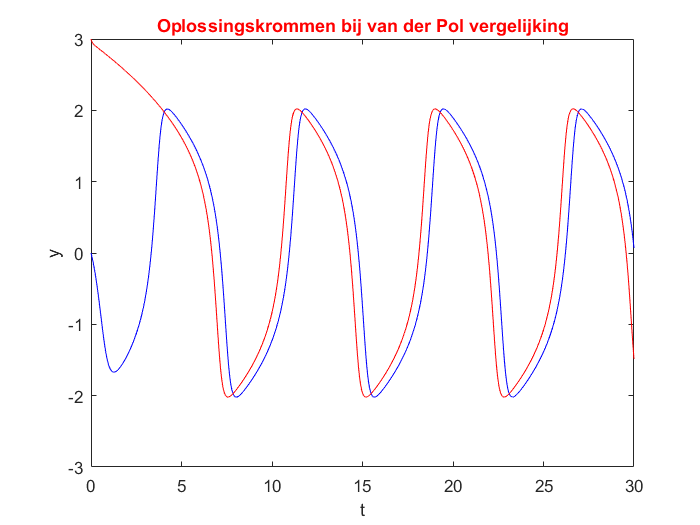

In the graphs we see that after a while a periodic solution is created. This is in fact a limit cycle.