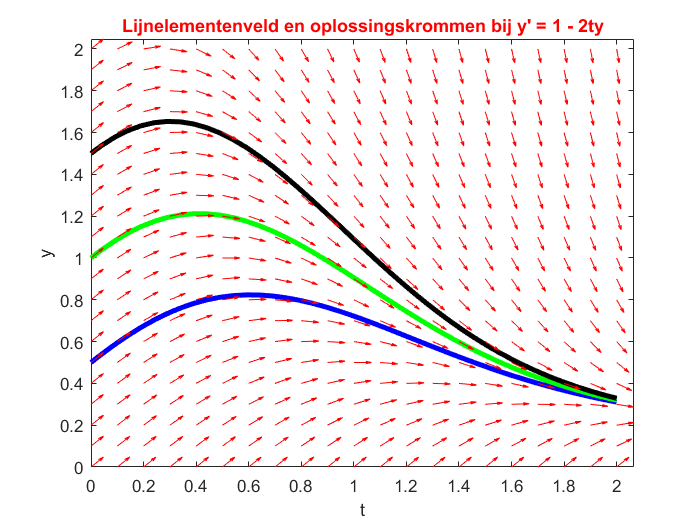
GDV van orde 1 We bekijken de differentiaalvergelijking \[\frac{\dd y}{\dd t}=1-2\,t\,y\] en berekenen numeriek oplossingskrommen bij beginwaarden \(y(0)=0.5\), \(y(0)=1\) en \(y(0)=1.5\). We tekenen de oplossingskrommen met een lijnelementenveld op de achtergrond.

Eerst maken we een M-bestand, gdv1.m, met de volgende inhoud.

function dydt = gdv1(t,y)
% bereken dydt = 1 - 2*t*y
    dydt = 1 - 2*t.*y;
end

Het enige wat dit script doet is waarden van \(t\) en \(y\) gebruiken om in het punt \((t,y)\) de afgeleide \(\frac{\dd y}{\dd t}\) te berekenen. Hierna kunnen we voor een gegeven tijdsdomein en verscheidene beginwaarden het bijpassende beginwaardeprobleem numeriek oplossen.

>> clear
>> opties = odeset('RelTol', 1e-5); % stel de nauwkeurigheid in
>> tdomein = [0,2];
>> y0 = [0.5, 1.0, 1.5];  % beginwaarden
>> [t,y] = ode45('gdv1', tdomein, y0, opties);
>> % grafieken van numerieke oplossing zijn te tekenen
>> plot(t, y(:,1), '-b', t, y(:,2), '-g', t, y(:,3), '-k', 'LineWidth', 3);
>> hold on
>> % voeg het lijnelementenveld toe
>> [t,y] = meshgrid(0:0.1:2, 0:0.1:2);
>> dy = 1 - 2*t.*y;
>> dt = ones(size(dy));
>> L = sqrt(dt.^2 + dy.^2);
>> dyu = dy./L;
>> dtu = dt./L;
>> quiver(t, y, dtu, dyu, 0.5, 'r'), axis tight
>> xlabel 't', ylabel 'y';
>> title("Lijnelementenveld en oplossingskrommen bij y' = 1 - 2ty",'Color','Red')

Van der Pol vergelijking Als voorbeeld van het numeriek oplossen van een GDV van orde 2 bekijken we de van der Pol vergelijking \[\frac{\dd^2y}{\dd t^2} -\frac{1}{\varepsilon}(1-y^2)\frac{\dd y}{\dd t}+y = 0\] met \(0<\varepsilon\ll 1\). Als voorbeeld nemen we een tamelijk grote waarde \(\varepsilon=\tfrac{1}{2}\) om duidelijker te kunnen laten zien wat er gebeurt. We berekenen numeriek oplossingskrommen bij beginwaarden \(y(0)=0, y'(0)=-1\) en bij \(y(0)=3, y'(0)=-1\).

Omdat de numerieke oplossingsmethode ode45 alleen werkt voor gewone differentiaalvergelijkingen van orde 1 of stelsels van 1ste orde differentiaalvergelijkingen, herformuleren we eerst de van der Pol vergelijking in een stelsel van twee gekoppelde 1ste orde differentiaalvergelijkingen. Introduceer \[y_1=y, y_2 = \frac{\dd y}{\dd t}\] dan geldt \[\frac{\dd y_2}{\dd t} = \frac{\dd^2y}{\dd t^2} = \frac{1}{\varepsilon}(1-y_1^2)\,y_2-y_1 \] Kortom, de van der Pol vergelijking stemt overeen met het volgende stelsel van 1ste orde differentiaalvergelijkingen \[\left\{\begin{aligned} \dfrac{\dd y_1}{\dd t} &= y_2\\ \dfrac{\dd y_2}{\dd t} &= \frac{1}{\varepsilon}(1-y_1^2)\,y_2-y_1 \end{aligned}\right.\] Eerst maken we daarom een M-bestand, gdv2.m, met de volgende inhoud.

function dydt = gdv2(t,y)
% van der Pol vergelijking met epsilon = 1/2
    dydt = [y(2); 2*(1-y(1)^2)*y(2)-y(1)];
end

Hierna kunnen we voor een gegeven tijdsdomein en verscheidene beginwaarden het bijpassende beginwaardeprobleem numeriek oplossen. Onderstaand diagram wordt door de volgende code verkregen.

>> clear
>> opties = odeset('RelTol', 1e-5); % stel de nauwkeurigheid in
>> tdomein = [0,30];
>> figure
>> y0 = [0,-1];  % eerste beginwaarden
>> [t,y] = ode45('gdv2', tdomein, y0, opties);
>> plot(t,y(:,1),'-b')
>> hold on
>> y0 = [3,-1];  % tweede beginwaarden
>> [t,y] = ode45('gdv2', tdomein, y0, opties);
>> plot(t,y(:,1),'-r')
>> xlabel 't', ylabel 'y';
>> title("Oplossingskrommen bij van der Pol vergelijking",'Color','Red')

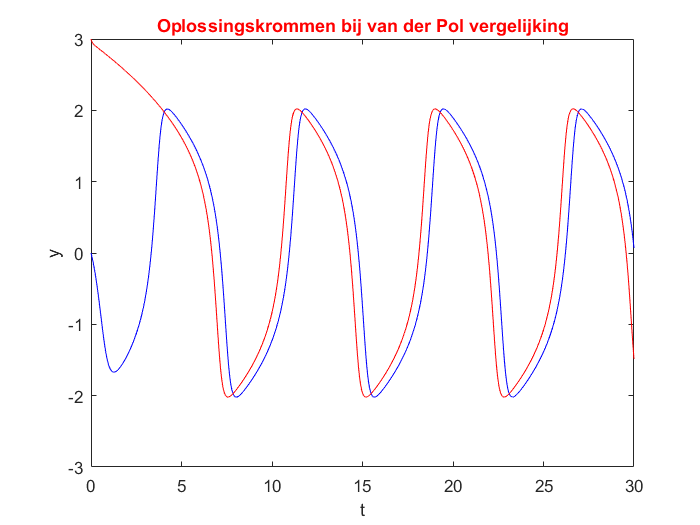
In de grafieken zien we dat er na een tijdje een periodieke oplossing ontstaat. Dit is in feite een limietcylus.