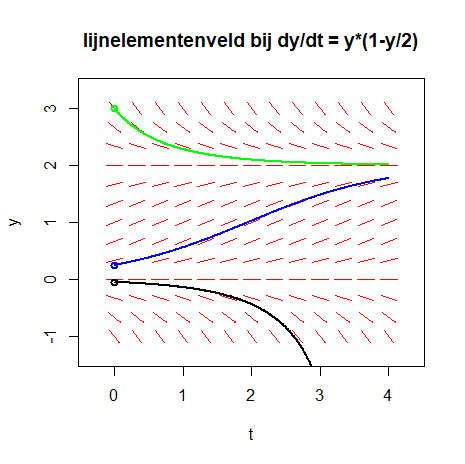
Het phaseR pakket heeft het flowField commando aan boord om het lijnelementenveld van een autonome differentiaalvergelijking van orde 1 te tekenen stelsel van twee differentiaalvergelijkingen te tekenen. We illustreren het gebruik van het R commando aan de hand van de logistische differentiaalvergelijking \[\frac{dy}{dt}=y\cdot (1-y/2)\] In dit lijnelementenveld tekenen we ook drie oplossingskrommen via het trajectory commando.

We specificeren in onderstaande code het beginwaardeprobleem in de vorm van een R functie met de volgende drie argumenten:

• de onafhankelijke variabele, waarbij wij meestal tijd \(t\) kiezen;
• de begintoestand van de afhankelijke variabele, waarbij het hier de grootheid \(y\) betreft;
• parameters, waarbij het hier om de parameters \(r\) en \(K\) gaat.

De functie levert een lijst van afgeleiden op, maar in dit geval is het enkel \(\frac{dy}{dt}\), en wordt gebruikt in de numerieke methode om de differentiaalvergelijking op te lossen. In onderstaand code fragment zorgt de instructie with(as.list(c(begintoestand, parameters)). ...) ervoor dat de namen van de parameters beschikbaar zijn in definitie van de differentiaalvergelijking.

library(phaseR)

# Definieer de diferentiaalvergelijking
model <- function(tijd, begintoestand, parameters){
  with(as.list(c(begintoestand, parameters)), {
    dydt <-  r*y*(1-y/K)
    return(list(dydt))
  })
}

params <- c(r = 1, K = 2) # specificeer de parameterwaarden

flowField(model, xlim = c(0, 4), ylim = c(-1, 3), 
          parameters = params, system = "one.dim",
          state.names = c("y"), points = 13, 
          arrow.head = 0.001, col = "red",
          add = FALSE, xlab = "t", ylab = "y",  
          main = "lijnelementenveld bij dy/dt = y*(1-y/2)")

trajectory(model, parameters = params, system = "one.dim",
           state.names = c("y"), y0 = c(0.25), tlim = c(0, 4), 
           col = "blue", lwd = 2)
trajectory(model, parameters = params, system = "one.dim",
           state.names = c("y"), y0 = c(3), tlim = c(0, 4), 
           col = "green", lwd = 2)
trajectory(model, parameters = params, system = "one.dim",
           state.names = c("y"), y0 = c(-0.05), tlim = c(0, 4), 
           col = "black", lwd = 2)

Bovenstaande R code tekent een lijnelementenveld samen met drie oplossingskrommen.

Bij niet-autonome differentiaalvergelijkingen moet je zelf het lijnelementenveld programmeren en combineren met grafieken van oplossingskrommen voor beginwaardeproblemen die berekend zijn met de R functie ode uit het deSolve pakket.

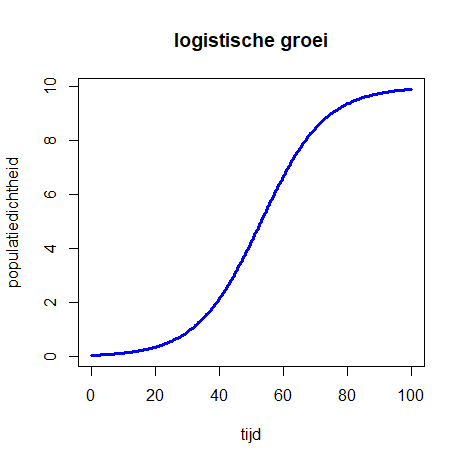
Als voorbeeld van het berekenen en tekenen van grafieken van oplossingskrommen bekijken we evenwel opnieuw het logistische groeimodel. We bekijken het beginwaardeprobleem \[\frac{dy}{dt}=r\cdot y\cdot (1-y/K), \quad y(0)=y_0\] voor \(r=0.1\) en \(K=10\).

Als beginwaarde, parameterwaarden, en het tijdsinterval kiezen we achtereenvolgens:

library(deSolve)

y0 <- c(y=0.05)    # beginwaarde van populatiedichtheid 
params <- c(r=0.1, # relatieve groeisnelheidsconstante r
            K=10)  # draagkracht K
t <- seq(from=0, to=100, by=0.5)  # tijdsinterval

Het groeimodel wordt nu opgelost met het ode commando:

oplossing <- ode(y0, t, model, params)

De uitvoer is een object met hierin een matrix die de waarden van de afhankelijke variabele bij opgegeven tijdstippen tabelleert. Je kunt hiermee een grafiek van de oplossingskromme tekenen. Wil je meer weten over hoe het beginwaardeprobleem numeriek precies is opgelost, toets dan het commando diagnostics(oplossing) in.

plot(oplossing, col="blue", main="logistische groei", 
     xlab="tijd", ylab="populatiedichtheid", lwd=3)

Bovenstaande R code levert onderstaand diagram op: