We consider the differential equation $$\frac{\dd y}{\dd t}=\frac{4-2t}{3y^2-5}$$

Assignments

1. Determine the general solution of the differential equation in implicit form by the method of separation of variables.
2. Draw a slope field and use the geom_contour function from the ggplot2 package to draw some integral curves in it.
   The result should resemble the figure below.

Worked-out solution

1. We write the differential equation in differential form and apply separation of variables: $$(3y^2-5)\,\dd y=(4-2t)\,\dd t$$ When we integrate on both sides we get $$\int (3y^2-5)\,\dd y=\int (4-2t)\,\dd t$$ So: $$y^3 -5y=4t-t^2+C$$ for some constant $C$. In other words, $$F(t,y)=C$$ where $$F(t,y)=y^3-5y+t^2-4t$$
2. You are asked to draw a slope field and some integral curves in one diagram. The last aspect concerns the drawing of contours of $$F(t,y)=y^3-5y+t^2-4t$$ The following code, in which the ggplot2 and dplyr packages are used, produces the diagram below:

   # load R packages
   library(dplyr)
   library(ggplot2)
   
   # prepare the computation of the slope field
   tp <- seq(from=-3, to=7, by=0.5)
   yp <- seq(from=-4, to=4, by=0.5)
   
   px <- c()
   py <- c()
   vx <- c()
   vy <- c()
   for(t in tp){
     for(y in yp){
       u <- 1.0
       v <- (4.0-2.0*t)/(3.0*y^2-5.0)
       L <- sqrt(u*u+v*v)
       u <- u/L
       v <- v/L
       px <- c(px, t-0.15*u)
       py <- c(py, y-0.15*v)
       vx <- c(vx, 0.3*u)
       vy <- c(vy, 0.3*v)
     }
   }
   d <- data.frame(x=px, y=py, vx=vx, vy=vy)
   
   # prepare the computation of the contour lines
   f <- function(t,y){ y^3-5*y+t^2-4*t }
   t <- seq(-3.5, 7.5, by=0.1)
   y <- seq(-4, 4, by=0.1)
   dat <- expand.grid(t = t, y = y) # make a grid for geom_countour
   dat <- mutate(dat, z = f(t, y)) # evaluate the function at each grid point
   
   # draw the slope fiweld with integral curves
   ggplot(dat, aes(t, y)) +
     geom_contour(aes(z = z), binwidth=6, colour="blue", size=1) +
     theme(panel.background = element_rect(fill = "white", colour = "grey50")) + 
     geom_segment(data=d, mapping=aes(x=px, y=py, xend=px+vx, yend=py+vy), colour="red") 

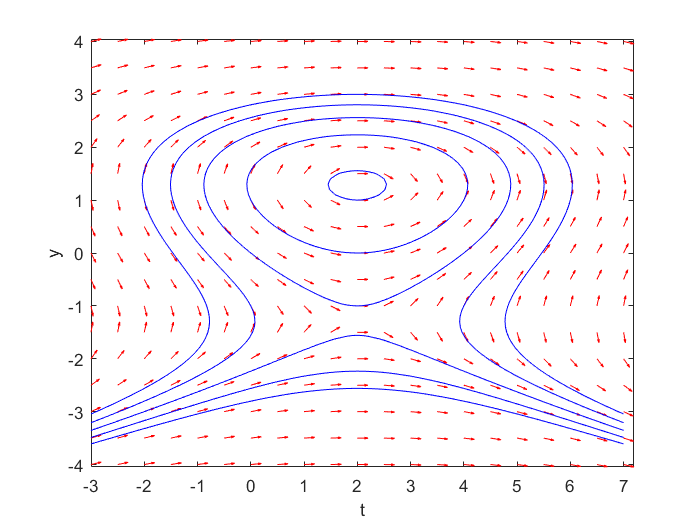
The integral curves describe more than one solution curve. The outer integral curve does this for 3 solution curves that depend on an initial value. We distinguish as solution curves

1. the top part with $y$ values greater than $\frac{1}{3}\sqrt{15}$;
2. the middle part with $y$ values between $-\frac{1}{3}\sqrt{15}$ and $\frac{1}{3}\sqrt{15}$;
3. the lower part smaller than $-\frac{1}{3}\sqrt{15}$