We bekijken de differentiaalvergelijking \[\frac{\dd y}{\dd t}=\frac{4-2t}{3y^2-5}\]

Opdrachten

1. Bepaal de algemene oplossing van de differentiaalvergelijking in impliciete vorm via de methode van scheiden van variabelen.
2. Teken een lijnelementenveld en teken daarin m.b.v de contour functie enkele integraalkrommen.

Uitwerking

1. We schrijven de differentiaalvergelijking in differentiaalvorm, waarbij we gelijk scheiding van variabelen toepassen: \[(3y^2-5)\,\dd y=(4-2t)\,\dd t\] Als we aan beide kanten integreren krijgen we \[\int (3y^2-5)\,\dd y=\int (4-2t)\,\dd t\] Dus: \[y^3 -5y=4t-t^2+C\] voor zekere constante \(C\). Met andere woorden \[F(t,y)=C\] voor \[F(t,y)=y^3-5y+t^2-4t\]
2. Er wordt gevraagd om een lijnelementenveld en enkelen integraalkrommen te tekenen in één diagram. Het laatste aspect betreft het tekenen van contourgrafiek van de functie \[F(t,y)=y^3-5y+t^2-4t\] De volgende code, waarin gebruik gemaakt wordt van de pakketten ggplot2 en dplyr, levert onderstaand diagram op:

   # laad R pakketten
   library(dplyr)
   library(ggplot2)
   
   # bereid de berekening van het lijnelementenveld voor
   tp <- seq(from=-3, to=7, by=0.5)
   yp <- seq(from=-4, to=4, by=0.5)
   
   px <- c()
   py <- c()
   vx <- c()
   vy <- c()
   for(t in tp){
     for(y in yp){
       u <- 1.0
       v <- (4.0-2.0*t)/(3.0*y^2-5.0)
       L <- sqrt(u*u+v*v)
       u <- u/L
       v <- v/L
       px <- c(px, t-0.15*u)
       py <- c(py, y-0.15*v)
       vx <- c(vx, 0.3*u)
       vy <- c(vy, 0.3*v)
     }
   }
   d <- data.frame(x=px, y=py, vx=vx, vy=vy)
   
   # bereid de berekening van contourlijnen voor
   f <- function(t,y){ y^3-5*y+t^2-4*t }
   t <- seq(-3.5, 7.5, by=0.1)
   y <- seq(-4, 4, by=0.1)
   dat <- expand.grid(t = t, y = y) # maak een rooster i.v.m. geom_countour
   dat <- mutate(dat, z = f(t, y)) # evalueer de functie op elk roosterpunt
   
   # teken het lijnelementenveld met integraalkrommen
   ggplot(dat, aes(t, y)) +
     geom_contour(aes(z = z), binwidth=6, colour="blue", size=1) +
     theme(panel.background = element_rect(fill = "white", colour = "grey50")) + 
     geom_segment(data=d, mapping=aes(x=px, y=py, xend=px+vx, yend=py+vy), colour="red") 
   

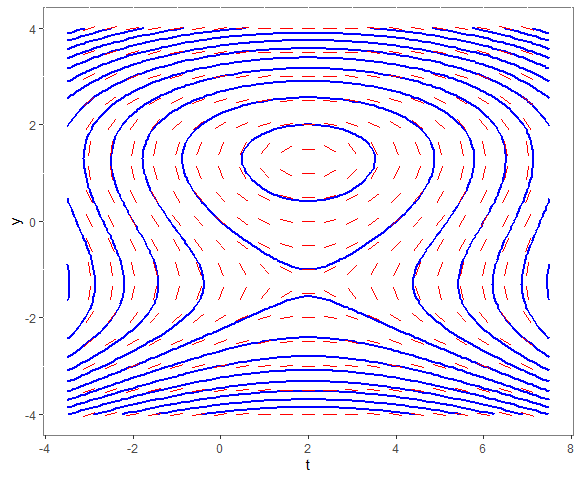
De integraalkrommen beschrijven meer dan één oplossingskromme. De buitenste integraalkromme doet dit voor 3 oplossingskrommen die afhangen van een beginwaarde. We onderscheiden als oplossingskrommen

1. het bovenste deel met \(y\)-waarden groter dan \(\frac{1}{3}\sqrt{15}\);
2. het middelste deel met \(y\)-waarden tussen \(-\frac{1}{3}\sqrt{15}\) en \(\frac{1}{3}\sqrt{15}\);
3. het onderste deel kleiner dan \(-\frac{1}{3}\sqrt{15}\)