Ordinary differential equations: Slope field and solution curves with R
 Forward Euler method [R worked-out solution]
Forward Euler method [R worked-out solution]
We consider the following initial value problems: \[\begin{aligned} \frac{\dd y}{\dd t}&=y\,(1-\tfrac{1}{3}y),\quad &y(-1)=.25\\ \\
\frac{\dd y}{\dd t}& =y\,(1-\tfrac{1}{3}y), &y(-1)=2.5\\ \\
\frac{\dd y}{\dd t}&=y\,(1-\tfrac{1}{3}y), &y(-1)=5.0\\ \\
\frac{\dd y}{\dd t}&=y\,(1-\tfrac{1}{3}y), &y(-1)=-0.25\end{aligned}
\] and draw a slope field of \[\frac{\dd y}{\dd t}=y\,(1-\tfrac{1}{3}y)\] with solution curves through the four given starting points.
The figure below is calculated with the following R script.
library(dplyr)
library(ggplot2)
Euler <- function(phi, t0, y0, t1, N=100) {
dt <- (t1-t0)/N
tn <- t0
yn <- y0
df <- data.frame(n=N, t=tn, y=yn)
for (k in 1:N) {
tn <- tn + dt
yn <- yn + phi(tn,yn)*dt
df <- rbind(df, data.frame(n=k+1, t=tn, y=yn))
}
return(df)
}
phi <- function(t,y) {
return(y*(1-y/3))
}
# compute points on four solution curves
df1 <- Euler(phi, -1, 0.25, 6, N=35)
df2 <- Euler(phi, -1, 2.50, 6, N=35)
df3 <- Euler(phi, -1, 5.00, 6, N=35)
df4 <- Euler(phi, -1, -0.25, 0.9, N=10)
# compute the slope field
tp <- seq(from=-2, to=6, by=0.5)
yp <- seq(from=-2, to=6, by=0.5)
d <- NULL
for(t in tp){
for(y in yp){
u <- 1.0
v <- phi(t,y)
L <- sqrt(u*u+v*v)
u <- u/L
v <- v/L
px <- t-0.15*u
py <- y-0.15*v
vx <- 0.3*u
vy <- 0.3*v
# data structure with coordinates of grid points and matching directions
d <- rbind(d, data.frame(x=px, y=py, vx=vx, vy=vy))
}
}
# maak diagram
fig <- ggplot(data.frame(x = c(-2, 6)), aes(x = t)) +
geom_segment(data=d, mapping=aes(x=x, y=y, xend=x+vx, yend=y+vy),
colour="red") +
geom_point(aes(t,y), data=df1, colour="blue") +
geom_path(aes(t,y), data=df1, colour="blue") +
geom_point(aes(t,y), data=df2, colour="black") +
geom_path(aes(t,y), data=df2, colour="black") +
geom_point(aes(t,y), data=df3, colour="green") +
geom_path(aes(t,y), data=df3, colour="green") +
geom_point(aes(t,y), data=df4, colour="magenta") +
geom_path(aes(t,y), data=df4, colour="magenta") +
theme_bw()
print(fig)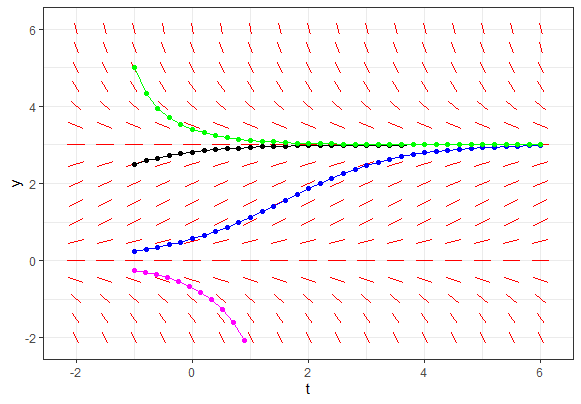
Unlock full access



