Existentie en uniciteit van oplossingen

Gewone differentiaalvergelijkingen: Lijnelementenveld en oplossingskrommen

Existentie en uniciteit van oplossingen

Gelet op de voorbeelden die tot nu toe behandeld zijn verbaast het wellicht dat het definitiegebied van een oplossing een rol speelt. Het is namelijk niet zo dat een oplossing van een beginwaardeprobleem altijd bestaat en evenmin dat deze dan uniek bepaald is of voor elke waarde van de onafhankelijke variabele gedefinieerd is.

Wiskundigen houden zich in het vakgebied van analyse van differentiaalvergelijkingen bij beginwaardeproblemen bezig met vragen over existentie (“Bestaat er minstens één oplossing en hoever reikt deze in de toekomst en het verleden?”) en uniciteit van beginwaardeproblemen ("Onder welke voorwaarden is er hoogstens één oplossing?"). Zo geldt bijvoorbeeld de volgende stelling:

Stelling van existentie en uniciteit. Stel dat de functies \(\varphi(t,y)\) en \(\displaystyle\frac{\partial \varphi(t,y)}{\partial y}\) continu zijn op een gesloten rechthoek \(R\) in het \(ty\)-vlak en dat \((t_0,y_0)\) een punt binnen \(R\) is en niet op de rand van \(R\) ligt. Dan heeft het beginwaardeprobleem \[\frac{\dd y}{\dd t}=\varphi(t,y),\quad y(t_0)=y_0\] een oplossing \(y(t)\) op een zeker \(t\)-interval waarbinnen zich \(t_0\) bevindt (existentie), maar ook niet meer dan één oplossing in de rechthoek \(R\) op elk \(t\)-interval dat \(t_0\) bevat (uniciteit).

Partiële afgeleide Partiële afgeleiden horen bij functies van meer variabelen. We lichten kort toe we ermee bedoelen. Je kunt bij een functie \(f(x,t)\) die afhangt van plaats \(x\) en tijd \(t\) één van de variabelen, zeg \(t\), constant houden. Je krijgt dan een functie die alleen \(x\) als onafhankelijke variabele heeft. Als deze functie 'net' is, kun je de afgeleide hiervan bepalen: deze afgeleide heet de partiële afgeleide van \(f(x,t)\) naar \(x\) van orde 1, die we noteren met \(\dfrac{\partial f(x,t)}{\partial t}\). Je kunt ook de partiële afgeleide weer als functie van twee variabelen zien en opnieuw partieel differentiëren. Dan krijg je partiële afgeleiden zoals: \[\frac{\partial^2 f(x,t)}{\partial x^2}=\frac{\partial}{\partial x}\left(\frac{\partial f(x,t)}{\partial x}\right)\quad\text{en}\quad \frac{\partial^2 f(x,t)}{\partial x \partial t}=\frac{\partial}{\partial x}\left(\frac{\partial f(x,t)}{\partial t}\right)\]

Voor \[f(x,y)=2x^2+3xy+4y^2\] geldt \[\begin{aligned} \frac{\partial f}{\partial x} &= 4x+3y \\ \\ \frac{\partial f}{\partial y} &= 3x+8y \\ \\ \frac{\partial^2 f}{\partial x^2} &= 4\\ \\ \frac{\partial^2 f}{\partial y^2} &= 8\\ \\ \frac{\partial^2 f}{\partial x\partial y} &= \frac{\partial^2 f}{\partial y\partial x}=3\end{aligned}\]

Als alle finesses van deze stelling niet duidelijk zijn is dat niet zo erg. Veel slordiger geformuleerd zegt deze stelling namelijk dat het beginwaardeprobleem \[\frac{\dd y}{\dd t}=\varphi(t,y),\quad y(t_0)=y_0\] een unieke oplossing op een zeker open interval \(I\), met \(t_0\in I\), mits de functie \(\varphi\) zich in de buurt van \((t_0,y_0)\) fatsoenlijk gedraagt. Zo'n interval kan zo groot mogelijk gekozen worden en dan spreekt men van het maximale existentie-interval.

Als aan de voorwaarden in de bovenstaande stelling niet voldaan is kan existentie en uniciteit wel een probleem zijn. Vier situaties passeren de revue:

geen oplossingen van een beginwaardeprobleem
meerdere oplossingen van een beginwaardeprobleem
'ontploffende' oplossingen en meerdere oplossingen voor de prijs van één formule
tot stilstand komende oplossingen

Geen oplossingen van een beginwaardeprobleem

Het beginwaardeprobleem \[\frac{\dd y}{\dd t}=\frac{1}{t},\quad y(0)=0\] heeft geen oplossing.
De algemene oplossing van \(\dfrac{\dd y}{\dd t}=\frac{1}{t}\) is \[y(t)=\ln\bigl(|t|\bigr)+c\] voor zekere constante \(c\). Maar in \(t=0\) is deze oplossing niet gedefinieerd.

De functie \(t\mapsto \frac{1}{t}\) gedraagt zich niet netjes rondom \(t=0\); sterker nog, is daar zelfs niet gedefinieerd. Aan de voorwaarden in de stelling is dus niet voldaan.

Meerdere oplossingen van een beginwaardeprobleem

Het beginwaardeprobleem \[\frac{\dd y}{\dd t}=\sqrt{y}, \quad y(0)=0\] heeft twee oplossingen: \[y(t)=t^2\quad\text{en}\quad y(t)=0\text.\]

De functie \(y\mapsto \sqrt{y}\) gedraagt zich niet netjes rondom \(y=0\); sterker nog, is links daarvan niet gedefinieerd. Aan de voorwaarden in de stelling is dus niet voldaan.

Bekijk het beginwaardeprobleem \[t \frac{\dd y}{\dd t}=y-t^2\cos t,\quad y(0)=0\] Er lijkt nog niets aan de hand, maar herschrijven van dit beginwaardeprobleem in de gedaante die gehanteerd is in de stelling voor existentie en uniciteit \[\frac{\dd y}{\dd t}=\frac{y}{t}-t\cos t\] lukt alleen voor \(t\neq 0\). Er kunnen dus problemen met existentie en uniciteit ontstaan als \(t=0\). Deze differentiaalvergelijking kan gelukkig ook exact opgelost worden en zo kan uitgezocht worden wat er aan de hand is. Schrijf bovenstaande GDV eerst in de volgende vorm: \[\frac{y'\cdot t-y}{t^2}=-\cos t\] Aan de linkerkant van deze vergelijkingstaat volgens de quotiëntregel voor differentiëren niets anders dan de afgeleide van \(\displaystyle\frac{y}{t}\). De rechterkant kan opgeschreven worden als de afgeleide van \(-\sin t\). Dus: \[\left(\frac{y}{t}\right)'=\left(-\sin t\right)'\] De afgeleiden aan de linker- en rechterkant van laatstgenoemde vergelijking zijn gelijk en dus zijn de functies waarvan de afgeleiden berekend worden op een constante na gelijk aan elkaar. Dus: \[\frac{y}{t}=c-\sin t,\] oftewel \[y=c\,t-t\sin t\] voor zekere constante \(c\). Echter, voor elke keuze van deze constante geldt \(y(0)=0\). Met andere woorden, het beginwaardeprobleem heeft oneindig veel oplossingen. Enkele oplossingskrommen van dit beginwaardeprobleem zijn tezamen met het lijnelementenveld in onderstaande figuur getekend.

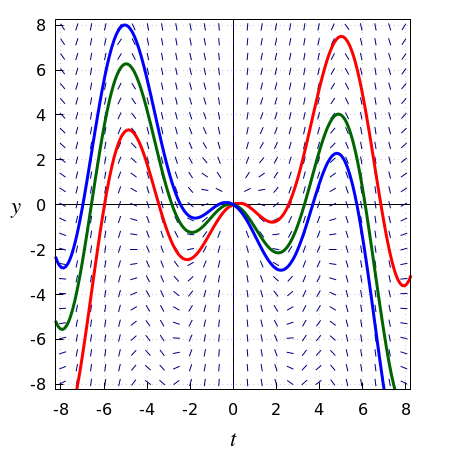
meerdere oplossingen

Vervang de beginwaarde \(y(0)=0\) in de GDV door \(y(0)=1\) en het beginwaardeprobleem heeft geen enkele oplossing.

'Ontploffende' oplossingen en meerdere oplossingen voor de prijs van één formule

Zelfs als existentie en uniciteit gegarandeerd is, blijkt het nog een interessante zaak om het maximale interval te bepalen waarop de oplossing van een beginwaardeprobleem bestaat. Dit existentie-interval hangt vaak af van de keuze van de beginwaarde. Er is dus eigenlijk sprake van lokale existentie: oplossingen van een beginwaardenprobleem hoeven niet te bestaan voor alle tijdstippen \(t\).

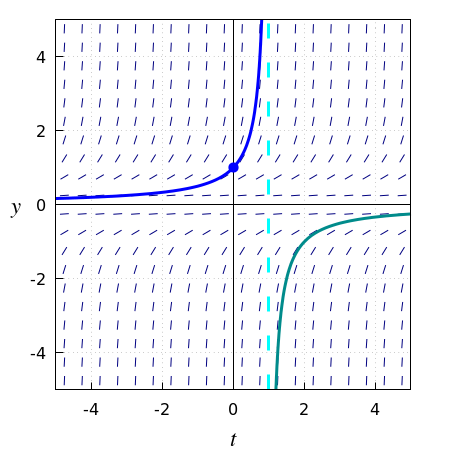
Bekijk het volgende beginwaardeprobleem: \[\frac{\dd y}{\dd t}=y^2,\quad y(0)=1\] Dan bestaat er een unieke oplossing \[y=\frac{1}{1-t}\] die ‘ontploft in een eindige tijd’, namelijk als \(t\) het tijdstip \(t=1\) nadert. Startend in \(t=0\) kan de oplossingskromme oneindig ver terug in de tijd gevolgd worden, maar in voorwaartse richting houdt het op bij \(t=1\); zie onderstaande figuur. Het heeft geen zin het deel van de grafiek van \(1/(1-t)\) rechts van \(t=1\) als oplossingskromme van het beginwaardeprobleem te beschouwen. Het is natuurlijk wel de oplossingskromme van het beginwaardeprobleem \(y'=y^2,\; y(2)=-1.\) Met andere woorden, één formule, \(1/(1-t)\), beschrijft twee oplossingen van de GDV \(y'=y^2.\)

twee exploderende oplossingen

Tot stilstand komende oplossingen

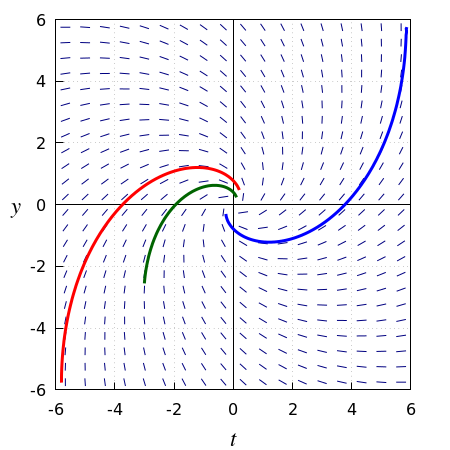
Bekijk de volgende differentiaalvergelijking:\[\frac{\dd y}{\dd t}=\frac{t+y}{t-y}\tiny.\] Het lijnelementenveld is in onderstaande figuur tezamen met enkele oplossingskrommen getekend. Wat opvalt is dat alle oplossingen over een begrensd interval gedefinieerd zijn en steeds van de ene rand van het maximale existentie-interval naar de andere rand gaan. De oplossingskrommen lopen spiraalvormig linksom weg van een vertrekpunt dicht op de lijn \(y=t\) naar een ander punt dicht op deze lijn; in beide punten is het bijpassende lijnelelement bijna verticaal.

tot stilstand komende oplossingen