Asymptotics

Ordinary differential equations: Asymptotics and stability

Asymptotics

In asymptotics of an initial value problem, it is all about the behaviour of solutions when the time \(t\) approaches one of its boundaries of the maximal interval of existence of the differential equation. It can simply be that solutions reach infinity in finite time, a phenomenon called blow-up, or it may involve the approach of a solution of a differential equation towards a specific solution in the course of time. The following examples illustrate the diversity of asymptotic behaviour of solutions of initial value problems.

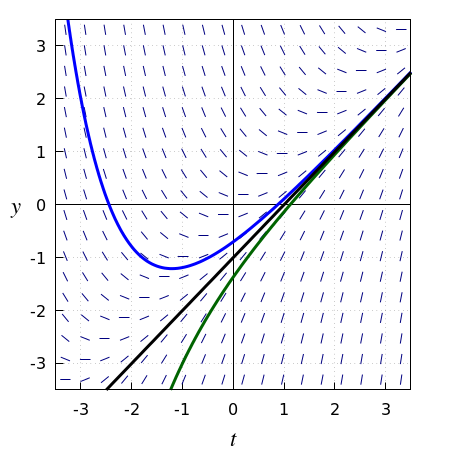
Consider the following differential equation: \[\frac{\dd y}{\dd t}=1+y^2\] The slope field of this differential equation is shown in the figure below, together with some solution curves. Do you recognize the green curve through \((0,0)\)? Indeed, this is the graph of the tangent function. The black dashed lines mark the endpoints of the maximal intervals of existence of this differential equation of width \(\pi\) for initial values \(y(k\cdot\pi)=0\) with some integer \(k\). The asymptotic behaviour of the solution \(y(0)=0\) is: \[\lim_{t\uparrow \frac{\pi}{2}}=\infty\quad\text{and}\quad \lim_{t\downarrow -\frac{\pi}{2}}=-\infty\] These limits mean in 'ordinary language' that the function values become plus or minus infinity when time \(t\) approaches the value \(\tfrac{1}{2}\pi\) from the left (from the bottom) and approaches the value \(-\tfrac{1}{2}\pi\) from the right (from the top).

asymptotiek van GDV voor de tangens functie

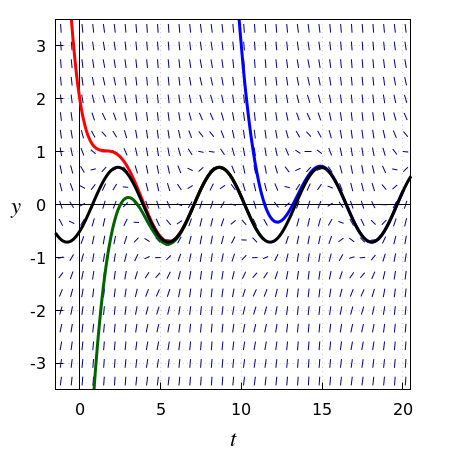
Consider the following differential equation: \[\frac{\dd y}{\dd t}=-y+\sin(t)\] The slope field of this differential equation is shown in the figure below, together with some solution curves. In this example, the asymptotic behaviour of each solution is the approach to a sinusoidal solution. The black solution curve is the plot of the specific solution \[y(t)=\tfrac{1}{2}\sqrt{2}\sin\left(t-\tfrac{1}{4}\pi\right)\] This is the only sinusoid that is a solution of this differential equation and all other solutions converge to this particular solution, that is, each solution behaves like a sinusoid after some time.

aymptotiek naar sinusgrafiek

The asymptotic behaviour is easier to understand when you realise that \[\frac{\dd y}{\dd t}=-y+\sin(t)\] is a non-homogeneous first-order linear differential equation. We already have a particular solution \[y_\text{part}(t)=\tfrac{1}{2}\sqrt{2}\sin\left(t-\tfrac{1}{4}\pi\right)\] and so the general solution is a sum of this particular solution and the general solution of the corresponding homogeneous ODE \[\frac{\dd y}{\dd t}=-y\] This is a differential equation of exponential decay with the general solution \[y(t)=c\cdot e^{-t}\] The general solution of the non-homogeneous ODE is \[y(t)=y_\text{part}+ c\cdot e^{-t}\] for some constant \(c\). Whatever value \(c\) has, it will always be true for the solution that \(y(t)\approx y_\text{part}\) for large \(t\).

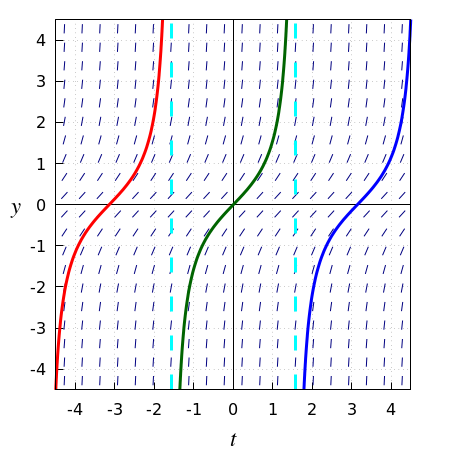
Consider the following differential equation: \[\frac{\dd y}{\dd t}=t-y\] The slope field of this differential equation is shown in the figure below, together with some solution curves. In this example, each solution curve approaches the graph of the solution \(y(t)=t-1\). The black solution curve is the plot of this particular solution.

lineaire asymptoot

The asymptotic behaviour can be explained by finding the exact solution of the differential equation. This can be done in the following way.

Suppose that a solution of the form \(y(t)=a\,t+b\) exists. Then: \[\frac{\dd y}{\dd t}=\frac{\dd}{\dd t}(a\,t+b)=a\] and \[\frac{\dd y}{\dd t}=t-y=t-(a\,t+b)=(1-a)\,t-b\] The equality \[a=(1-a)t+b\] for all \(t\) leads to two equation: \[1-a=0\quad\text{and}\quad a = -b\] The second equation follows, for example, from the substitution of \(t=0\). Using this this result and substitution of \(t=1\) leads to the first equation. Thus: \[a=1,\;b=-1\] So, the straight line with equation \(y=t-1\) is a solution curve of the differential equation.
Suppose that \[y(t)=z(t)+t-1\] is a solution of the differential equation. Then: \[\frac{\dd y}{\dd t}=\frac{dz}{dt}+1\] and \[\frac{\dd y}{\dd t}=t-y=t-(z+t-1)=(1-z)\] So: \[\frac{dz}{dt}=-z\] This is the differential equation of exponential decay and has the general solution \[z(t)=c\,e^{-t}\] for some constant \(c\). So, the general solution of the original differential equation is given by \[y(t)=C\,e^{-t}+t-1\] The first term is negligibly small for large values of \(t\), and thus \[y(t)\approx t-1 \text{ for large } t\]