Asymptotiek

Gewone differentiaalvergelijkingen: Asymptotiek en stabiliteit

Asymptotiek

Bij asymptotiek van een beginwaardeprobleem handelt het om het gedrag van oplossingen wanneer de tijd \(t\) een van de grenzen van het maximale existentie-interval nadert. Het kan simpelweg gaan om het ‘ontploffen’ van een oplossing, maar ook kan het gaan om het naderen van een specifieke oplossing. De volgende voorbeelden illustreren de diversiteit van asymptotisch gedrag van oplossingen van beginwaardenproblemen.

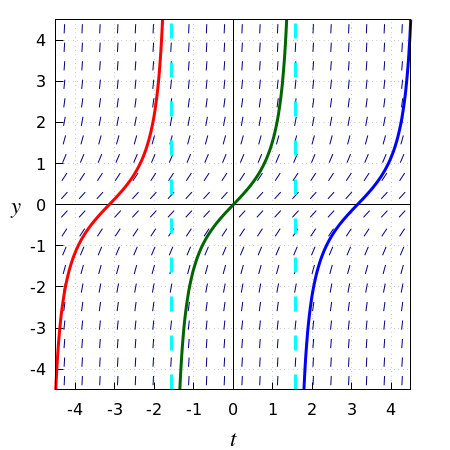
Bekijk de volgende differentiaalvergelijking: \[\frac{\dd y}{\dd t}=1+y^2\] Het lijnelementenveld van deze differentiaalvergelijking is in onderstaande figuur tezamen met enkele oplossingskrommen getekend. Komt de groene kromme door \((0,0)\) je niet bekend voor? Inderdaad: dit is de grafiek van de tangens. De zwarte stippellijnen markeren de randen van maximale existentie-intervallen van breedte \(\pi\) bij beginwaarden \(y(k\cdot\pi)=0\) voor gehele getallen \(k\). Het asymptotisch gedrag van de oplossing met \(y(0)=0\) is als volgt: \[\lim_{t\uparrow \frac{\pi}{2}}=\infty\quad\text{en}\quad \lim_{t\downarrow -\frac{\pi}{2}}=-\infty\] Deze limieten betekenen in 'gewone' woorden dat de functiewaarden plus of min oneindig worden wanneer de tijd \(t\) de waarde \(\tfrac{1}{2}\pi\) van de linkerkant (onderkant) nadert respectievelijk \(-\tfrac{1}{2}\pi\) van de rechterkant (bovenkant) nadert.

asymptotiek van GDV voor de tangens functie

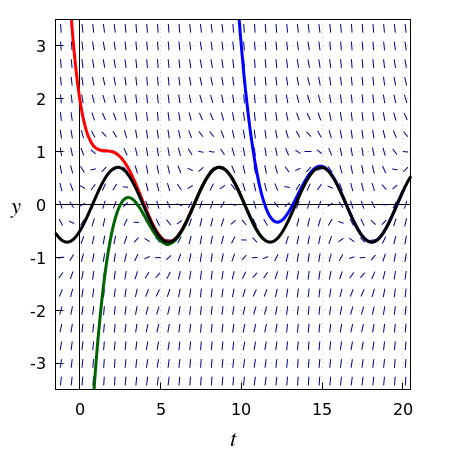
Bekijk de volgende differentiaalvergelijking: \[\frac{\dd y}{\dd t}=-y+\sin(t)\] Het lijnelementenveld van deze differentiaalvergelijking is in onderstaande figuur tezamen met enkele oplossingskrommen getekend. In dit voorbeeld is het asymptotisch gedrag van elke oplossingskromme dat van een sinusvormige grafiek. De zwarte oplossingskromme hoort bij de speciale oplossing \[y(t)=\tfrac{1}{2}\sqrt{2}\sin\left(t-\tfrac{1}{4}\pi\right)\] Dit is de enige sinusoïde die een oplossing van deze differentiaalvergelijking is en tevens convergeren alle andere oplossingen naar deze speciale oplossing, dat wil zeggen, na verloop van tijd gedraagt een oplossing zich altijd als een sinusoïde.

aymptotiek naar sinusgrafiek

Het asymptotisch gedrag is beter te begrijpen als je je realiseert dat \[\frac{\dd y}{\dd t}=-y+\sin(t)\] een eerste-orde lineaire inhomogene differentiaalvergelijking is. We hebben al een particuliere oplossing \[y_\text{part}(t)=\tfrac{1}{2}\sqrt{2}\sin\left(t-\tfrac{1}{4}\pi\right)\] en dus is de algemene oplossing een som van deze specifieke oplossing en de algemene oplossing van de bijpassende homogene GDV \[\frac{\dd y}{\dd t}=-y\] Dit is een differentiaalvergelijking van exponentieel verval met de algemene oplossing \[y(t)=c\cdot e^{-t}\] De algemene oplossing van de inhomoge GDV is dus \[y(t)=y_\text{part}+ c\cdot e^{-t}\] Voor elke constante \(c\) zal gelden dat \(y(t)\approx y_\text{part}\) voor grote \(t\).

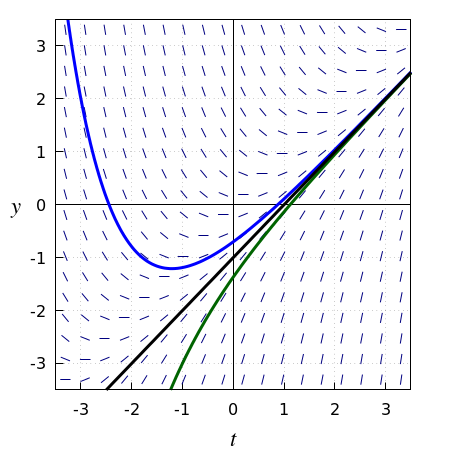
Bekijk de volgende differentiaalvergelijking: \[\frac{\dd y}{\dd t}=t-y\] Het lijnelementenveld van deze differentiaalvergelijking is in onderstaande figuur tezamen met enkele oplossingskrommen getekend. In dit voorbeeld nadert elke oplossingskromme de oplossing \(y(t)=t-1\). De zwarte oplossingskromme hoort bij deze speciale oplossing.

lineaire asymptoot

Door de exacte oplossing van de differentiaalvergelijking op te sporen is het aymptotisch gedrag wel te verklaren. Dit kan op de volgende manier gebeuren.

Stel dat een oplossing van de vorm \(y(t)=a\,t+b\) bestaat. Er geldt dan: \[\frac{\dd y}{\dd t}=\frac{\dd}{\dd t}(a\,t+b)=a\] en \[\frac{\dd y}{\dd t}=t-y=t-(a\,t+b)=(1-a)\,t-b\] Deze twee vergelijkingen moeten gelden voor alle \(t\) en dit levert twee eisen op: \[1-a=0\quad\text{en}\quad a = -b\] Ofwel: \[a=1,\;b=-1\] Dus, de rechte lijn met vergelijking \(y=t-1\) is een oplossingskromme van de differentiaalvergelijking.
Stel nu dat \[y(t)=z(t)+t-1\] ook een oplossing is van de differentiaalvergelijking. Er geldt dan: \[\frac{\dd y}{\dd t}=\frac{dz}{dt}+1\] en \[\frac{\dd y}{\dd t}=t-y=t-(z+t-1)=(1-z)\] Dus geldt: \[\frac{dz}{dt}=-z\] Dit is de differentiaalvergelijking van exponentieel verval en die heeft als algemene oplossing \[z(t)=c\,e^{-t}\] voor zekere constante \(c\). Dus is de algemene oplossing van de oorspronkelijke differentiaalvergelijking gegeven door: \[y(t)=c\,e^{-t}+t-1\] Voor grote \(t\) is de eerste term verwaarloosbaar klein en er geldt dus: \[y(t)\approx t-1 \text{ voor grote } t\]