The forward Euler method

Ordinary differential equations: Slope field and solution curves

The forward Euler method

Forward Euler method The geometric approach to solving a first-order dynamical system of the form \[\frac{\dd y}{\dd t}=\varphi(t,y)\] with initial value \[y(t_0)=y_0\] via a slope field, according to the motto 'go with the flow', leads to the forward Euler method for computing a numerical solution a GDV.

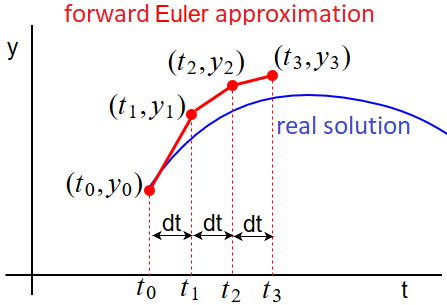
Let \((t_0, y_0)\) be a point on the solution curve.
Suppose that you want to know the solution at time \(t_1=t_0+dt\) for some time step \(dt\).
If \(dt\) is small, you can approximate the graph of the function near \((t_0, y_0)\) by the tangent line \(y=y_0+y'(t_0)\cdot (t-t_0)=y_0+\varphi(t_0,y_0)\cdot (t-t_0)\).
Then you can approximate at \(t_1=t_0+dt\) the function value \(y(t_1)\) with \(y(t_1)\approx y_1= y_0+\varphi(t_0,y_0)\cdot dt\).

This method can be repeated with time \(t_2=t_1+dt\) and \(\bigl(t_1, y_1\bigr)\) as starting point.
Then: \(y(t_2)\approx y_2=y_1+\varphi(t_1,y_1)\cdot dt\).

One more time for \(t_3=t_2+dt\) and \(\bigl(t_2, y_2\bigr)\) as starting point.
Then: \(y(t_3)\approx y_3=y_2+\varphi(t_2,y_2)\cdot dt\).

You can continue this approximation process as long as you wish: \[t_k=t_0+k\cdot dt\quad\text{and}\quad y_{k+1}=y_k+\varphi(t_k,y_k)\cdot dt,\qquad\text{for }k=0,1,2,3,\ldots\]

The figure below shows how the approximations indeed differ from the actual solution curve, but for small steps \(dt\) the error will be limited.

forward Euler approximation

The forward Euler method is based on the iterative formula \[\eta_{k+1}=\eta_k+\varphi(t_k,\eta_k)\cdot dt\] where \(dt\) is the chosen step size, \(\varphi(t,y)\) is the right-hand side of the differential equation, and the points \(t_k\) are selected at equal distance from each other, depending on the step size using the formula \[t_k=t_0+k\cdot dt\] for \(k=0,1,2,\ldots,n\). Initially you start with \({\eta}_0=y_0\) at time \(t_0\) and determine \(\eta_1\) as approximation of \(y(t_1)\) by using the tangent at the point \((t_0,\eta_0)\) as an approximation to the graph of the solution \(y\) in the segment \([t_0,t_1]\): \[\eta_1=\eta_0+\varphi(t_0,\eta_0)\cdot dt\] Starting with the newly computed point \((t_1,\eta_1)\) you can approximate the function value \(y(t_2)\) with \(\eta_2\) via: \[\eta_2=\eta_1+\varphi(t_1,\eta_1)\cdot dt\] This approximation process can be repeated as often as you want and this leads to the formula for \(\eta_{k+1}\).

In the figure below, the function values calculated for the initial value problem \(\frac{dy}{dt}=-0.7y,\; y(0)=6\) are shown in a line graph for the step size \(dt=1\).

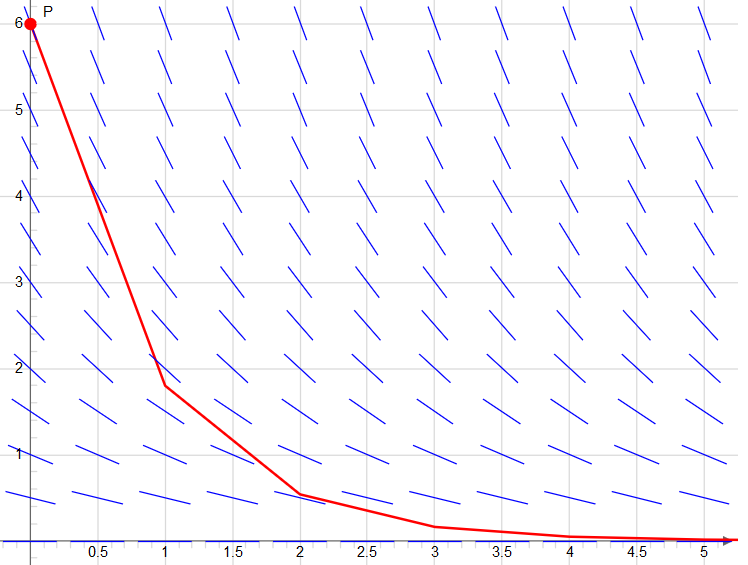
Formula \(\eta_{k+1}=\eta_k+\varphi(t_k,\eta_k)\cdot dt\) is in this particular case equal to \[\eta_{k+1}=\eta_k+r\cdot \eta_k\cdot dt=\eta_k(1+r\cdot dt)=\eta_0(1+r\cdot dt)^{k+1}\] with \(r=-0.7, \eta_0=6\). The exact solution of this initial value problem is \(y(t)=6e^{-0.7t}\).

As the step size \(dt\) becomes smaller in the Euler method, the graph of the calculated function values becomes smoother and is increasingly more resemblant to the graph of an exact solution.

Interactive computer version of Euler's method As the step size \(dt\) becomes smaller in the Euler method, the graph of the calculated function values becomes smoother and is increasingly more resemblant to the graph of an exact solution. To experience this for yourself, you can use the interactive version of the Euler method at the bottom of this page in the digital module; play with it and learn!