De voorwaartse Euler methode

Gewone differentiaalvergelijkingen: Lijnelementenveld en oplossingskrommen

De voorwaartse Euler methode

De meetkundige aanpak van het oplossen van een dynamisch systeem van eerste orde van de vorm $\frac{\dd y}{\dd t}=\varphi(t,y)$ met beginwaarde $y(t_0)=y_0$ via een lijnelementenveld, volgens het motto 'ga met de stroom mee, leidt tot de voorwaartse Euler methode voor het bepalen van een numerieke oplossing van een GDV.

Stel dat $(t_0, y_0)$ een punt op de oplossingskromme is.
Stel nu dat je de oplossing op tijdstip $t_1=t_0+dt$ wilt weten voor een zekere tijdstap $dt$ .
Als $dt$ klein is kun je de grafiek van de functie in de buurt van $(t_0, y_0)$ benaderen met de raaklijn $y=y_0+y'(t_0)\cdot (t-t_0)=y_0+\varphi(t_0,y_0)\cdot (t-t_0)$ .
Dan geldt voor $t_1=t_0+dt$ dat we $y(t_1)$ kunnen benaderen met $y(t_1)\approx y_1= y_0+\varphi(t_0,y_0)\cdot dt$ .

Dit spel kunnen we herhalen met tijdstip $t_2=t_1+dt$ en $\bigl(t_1, y_1\bigr)$ als startpunt.
Dan: $y(t_2)\approx y_2=y_1+\varphi(t_1,y_1)\cdot dt$ .

Een nog een keer herhaald met tijdstip $t_3=t_2+dt$ en $\bigl(t_2, y_2\bigr)$ als startpunt.
Dan: $y(t_3)\approx y_3=y_2+\varphi(t_2,y_2)\cdot dt$ .

Zo kun je verder gaan: $t_k=t_0+k\cdot dt\quad\text{en}\quad y_{k+1}=y_k+\varphi(t_k,y_k)\cdot dt\text{,}\qquad\text{voor }k=0,1,2,3,\ldots$

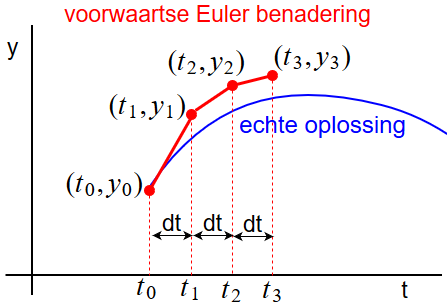
Onderstaande figuur laat zien hoe de benaderingen weliswaar afwijken van de echte oplossingskromme, maar voor kleine stapjes $dt$ zal de fout beperkt blijven.

De voorwartse Euler methode is gebaseerd op de iteratieve formule $\eta_{k+1}=\eta_k+\varphi(t_k,\eta_k)\cdot dt$ waarbij $dt$ de gekozen stapgrootte is, $\varphi(t,y)$ het rechterlid van de differentiaalvergelijking is en de punten $t_k$ op gelijke afstand gekozen zijn, afhankelijk van de stapgrootte via de formule $t_k=t_0+k\cdot dt$ voor $k=0,1,2,\ldots,n$ . In eerste instantie begin je dus met ${\eta}_0=y_0$ op tijdstip $t_0$ en bepaal je $\eta_1$ als benadering voor $y(t_1)$ door de raaklijn in het punt $(t_0,\eta_0)$ te gebruiken als benadering voor de grafiek van de oplossing $y$ op het segment $[t_0,t_1]$ : $\eta_1=\eta_0+\varphi(t_0,\eta_0)\cdot dt$ Uitgaande van het nu bekende punt $(t_1,\eta_1)$ kan je de volgende functiewaarde $y(t_2)$ benaderen met $\eta_2$ via: $\eta_2=\eta_1+\varphi(t_1,\eta_1)\cdot dt.$ Dit benaderingsproces herhaal je zo vaak je wil en dit leidt tot de algemene formule voor $\eta_{k+1}$ .

In onderstaande figuur zijn de zo berekende functiewaarden voor het beginwaardeprobleem $\frac{dy}{dt}=-0.7y,\; y(0)=6$ in een lijngrafiek te zien voor een stapgrootte $dt=1$ .

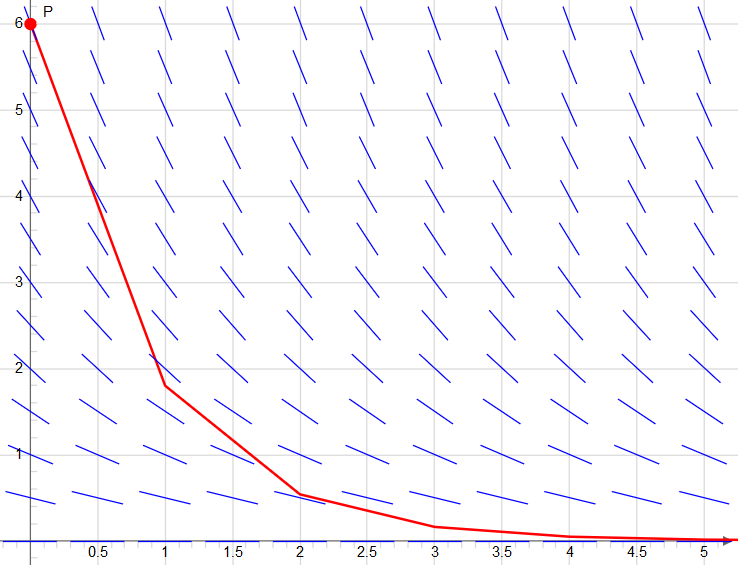
Formule $\eta_{k+1}=\eta_k+\varphi(t_k,\eta_k)\cdot dt$ is in dit specifieke geval gelijk aan $\eta_{k+1}=\eta_k+r\cdot \eta_k\cdot dt=\eta_k(1+r\cdot dt)=\eta_0(1+r\cdot dt)^{k+1}$ met $r=-0.7, \eta_0=6$ . De exacte oplossing van dit beginwaardeprobleem is $y(t)=6e^{-0.7t}$ .

Naarmate de stapgrootte $dt$ kleiner is in de Euler methode, wordt de grafiek van de berekende functiewaarden gladder en begint deze steeds meer op de grafiek van een exacte oplossing te lijken.

Naarmate de stapgrootte $dt$ kleiner is in de Euler methode, wordt de grafiek van de berekende functiewaarden gladder en begint deze steeds meer op de grafiek van een exacte oplossing te lijken. Om dit zelf te ervaren is in de digitale module een interactieve versie van de Eulermethode onderaan deze pagina te vinden; speel er mee en leer!