Pharmacokinetics The way in which a substance is administered to the human body is important in pharmacokinetics. The painkiller morphine for example, may be administered in various ways to a patient: orally (via a pill), by injections (subcutaneous, into a muscle, or directly into the bloodstream), or by infusion. This has major implications for the uptake, distribution, and operation of the substance in the body.

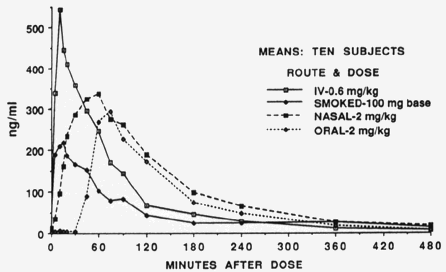
In an oral administration of morphine, the substance must first pass through the liver, but this organ lets a limited part go into the central circulation of the body. In other words, by oral administration of morphine, the bioavailability of this substance is low (about 40%), especially compared to administration by intravenous bolus injection (i.e., by an injection of the substance directly into a blood vein) with a bioavailability of almost 100%. The figure below illustrates another example: the way in which cocaine is used plays a major role in the time course of the concentration of the substance in the blood plasma. Upon injection or smoking, a high peak plasma concentration is reached after a few minutes, whereas with oral administration only after half an hour an increase in the plasma concentration is observed and the peak is reached after more than one hour.

In this example, we will study a simple model of an orally administered drug and see how the method of an integrating factor yields an exact solution of the model.

Oral administration, i.e., swallowing tablets or consuming medicinal drink, is the most used form of drug delivery. The drug first comes in contact with the stomach. With some delay the drug then goes into the small intestine; The delay is seen in a concentration-time curve, as the concentration starts to rise some time \((t_{lag}\) ) after oral administration. In the mathematical model we will ignore this delay by pretending all drug has already reached the small intestine at time \(t=0\) and the absorption of the drug will start from that moment. From the small intestine the drug comes through the portal vein into the liver via a diffusion process. The absorption process into the blood follows mainly first-order kinetics due to passive diffusion. The liver only lets a limited part continue unchanged into the general circulation of the body (beyond the portal vein and liver). Via the blood the drug spreads subsequently further through the body and can do its therapeutic effect.

As soon as the absorbed drug is distributed over the body, it is also undergoing a process of elimination. In the beginning, the absorbed amount exceeds the eliminated amount with the result that the plasma concentration is increasing. At the maximum, the absorption rate is as large as the elimination rate. After some time, when the absorption process is nearing its end, the elimination predominates; The concentration then decreases over time. The graph below shows the typical shape of concentration-time curve for an orally administered drug.

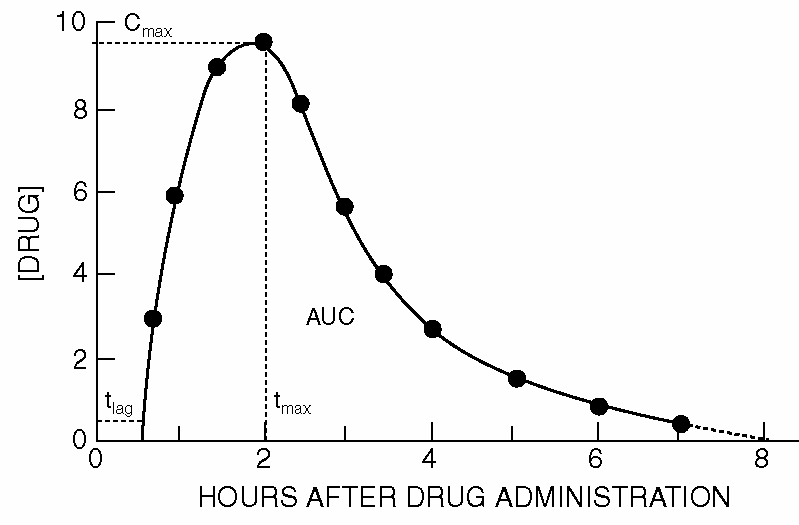
The fraction of the administered drug that reaches the general circulation unchanged is called the bioavailability of the drug in the Dutch literature. This quantity is commonly referred to with the capital letter \(F\) in formulas. In addition, the speed of absorption plays a role in determining the quality of a therapeutic drug. The US definition for 'bioavailablity' includes both facets, rate and extent of absorption. The term 'absolute bioavailablity' denotes the fraction of the substance that is absorbed. A low bioavailability of a drug can have various causes, including: poor water solubility (leading to the incomplete dissolution of a substance), degradation in the gastrointestinal tract, incomplete release because of an inadequate type of administration, "first pass metabolism" in the liver (i.e., biotransformation after the first or several passages in the liver), and interactions with other substances (e.g., other drugs) in the body. The bioavailability of a drug which is susceptible to rapid biotransformation during passage of the intestinal wall and liver will be low. For example, 60-80% of an oral dose of the beta blocker propranolol during the first passage is blocked by the liver. To determine the bioavailability, the concentration in the blood, serum or plasma is usually measured over time and in particular, the area under the concentration-time curve (AUC, area under the curve) is calculated. The area from time zero to infinity is a widely used measure of the biological activity. The formula used for an open one-compartment model is then: \[F=\frac{\mathrm{AUC}\cdot \mathrm{Cl}}{D}\] where \(D\) is the dose administered and \(\mathrm{Cl}\) the clearance of the drug. As a measure of the rate at which a drug is subject to the peak levels \(C_\mathrm{max}\) and duration \(C_\mathrm{max}\) which this is achieved.

ODE of plasma concentration of a drug when administered orally In the remainder of this theory page we assume an open one-compartment model with first-order kinetics for both the absorption and elimination phase, with an absorption rate constant \(k_a\) and elimination rate constant \(k\). It will be shown that the course of the plasma concentration of a drug, with the proviso that the absorption rate constant is greater than the elimination rate constant, is mathematically described by a bi-exponential function, with a term for absorption and elimination. The figure below shows a graphic representation of the model for oral administration of a drug with first-order kinetics for absorption into and elimination from the body, considered as a single central compartment:

This picture suggests the following: the drug is absorbed from the small intestine and passed through the liver to the general circulation, but only partly. For the reduction of the drug from the small intestine, we use an exponential model with elimination rate constant \(k_a\). So \[\frac{\dd A_\mathrm{small\;intenstine}}{\dd t}=-k_a\cdot A_\mathrm{small\;intenstine}\] with \(A_\mathrm{small\;intenstine}\) the amount of drug in the small intestine. The speed at which it gets into the general blood circulation is of opposite sign and only a fraction \(F\) of the drug passes through the small intestine and liver. In formula form, the absorption component of the change in amount of drug in the central component is equal to the following: \[\left(\frac{\dd A_\mathrm{central\;compartment}}{\dd t}\right)_\mathrm{absorption}= F\cdot k_a\cdot A_\mathrm{small\;intenstine}\] The first-order kinetics of elimination can be written in mathematical language as \[\left(\frac{\dd A_\mathrm{central\;compartment}}{\dd t}\right)_\mathrm{elimination}= -k\cdot A_\mathrm{central\;compartment}\] Addition of the formulas for absorption and elimination gives a formula for the change of the drug in the central compartment, and, along with the formula for elimination from the small intestine, a pair of equations describing the change of amounts of drug in the small intestine and the central component together: \[\begin{aligned} \frac{\dd A_\mathrm{small\;intestine}}{\dd t} &=-k_a\cdot A_\mathrm{small\;intestine}\\ \\ \frac{\dd A_\mathrm{central\;compartment}}{\dd t}&=F\cdot k_a\cdot A_\mathrm{small\;intestine}-k\cdot A_\mathrm{central\;compartment}\end{aligned}\] Division by the volume of distribution \(V_d\) of the central compartment gives a system of equations in terms of the amount of drug in the small intestine and plasma concentration \(C\) : \[\begin{aligned} \frac{\dd A_\mathrm{small\;intestine}}{\dd t} &=-k_a\cdot A_\mathrm{small\;intestine}\\ \\ \frac{\dd C}{\dd t}&=\frac{F\cdot k_a}{V_d}\cdot A_\mathrm{small\;intestine}-k\cdot C\\ \end{aligned}\] The first equation is an ODE for exponential decay, and has as a solution \[A_\mathrm{small\;intestine}=A_0\,e^{-k_a\,t}\] where \(A_0\) is the initial amount of the drug in the small intestine and therefore equal to the administered dose of the drug. Substituting this formula gives in the second equality: \[\frac{dC}{\dd t}=\frac{F\cdot k_a\cdot A_0}{V_d}\cdot e^{-k_a\,t}-k\cdot C\] This equation is of the following form: \[\frac{\dd C}{\dd t}=\alpha e^{-k_a\,t}-k\cdot C\] for some constant \(\alpha=(F\cdot k_a\cdot A_0)/V_d\).

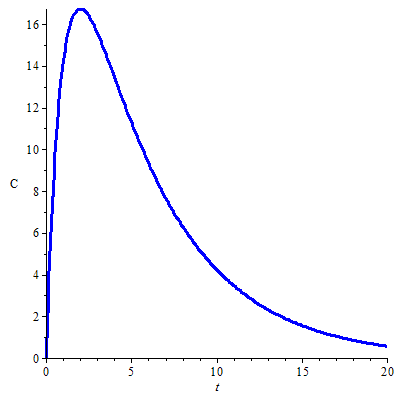
Computation of the concentration-time profile The differential equation \[\frac{\dd C}{\dd t}=\alpha e^{-k_a\,t}-k\cdot C,\] for certain constant \(\alpha\), can be solved by using an integrating factor. First we rewrite the equation in differential form as \[\dd C+k\,C\,\dd t=\alpha e^{-k_a\,t}\,dt\] Multiplying by the integrating factor \(e^{k\,t}\) gives \[e^{k\,t}\,\dd C+k\,e^{k\,t}\,C\,\dd t=\alpha e^{(k-k_a)t}\,\dd t\] The left- and right-hand sides of the equation are differentials of functions; if \(k\neq k_a\) then \[\dd\left(e^{k\,t}\,C\right)=\dd\left(\frac{\alpha}{k-k_a}\,e^{(k-k_a)t}\right)\] It follows that \[e^{k\,t}\,C=\frac{\alpha}{k-k_a}\,e^{(k-k_a)t}+\beta\] Thus \[C=\frac{\alpha}{k-k_a}\,e^{-k_a\,t}+\beta e^{-k\,t}\] for some integration constant \(\beta\). If \(C(0)=0\), then \(\alpha/(k-k_a)+\beta=0\), i.e., \(\beta=\alpha/(k_a-k)\), and the solution of the GDV can be written as \[C=\frac{\alpha}{k_a-k}\left(e^{-k\,t}- e^{-k_a\,t}\right).\] We have found the following general formula for the plasma concentration \(C\) under the condition that \(k\neq k_a\): \[C=\frac{k_a A_0 F }{V_d{(k_a-k)}}\left(e^{-k\,t}- e^{-k_a\,t}\right)\] This is a bi-exponential function . The figure below shows the graph of the plasma concentration of a drug calculated for the following pharmacokinetic parameters: \[\text{oral dose }A_0=500\,\mathrm{mg},\; k_a=1.0\,\mathrm{h}^{-1},\; k=0.2\,\mathrm{h}^{-1}, \;V_d=10\,\mathrm{L}, F=0.5\]