Farmacokinetiek De manier waarop een stof aan het menselijk lichaam wordt toegediend is belangrijk in de farmacokinetiek. De pijnbestrijdende stof morfine kan bijvoorbeeld op verschillende wijzen toegediend worden aan een patiënt: oraal (via een pilletje), via inspuitingen (onderhuids, in een spier of rechtstreeks in de bloedbaan) of via een infuus. Dit heeft grote gevolgen voor de opname, distributie, en werking van de stof in het lichaam.

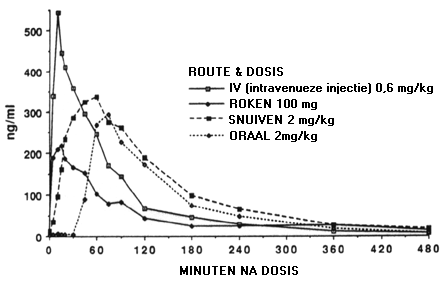
Bij een orale toediening van morfine moet deze stof eerst de lever passeren, maar dit orgaan laat maar een beperkt deel doorgaan naar de centrale circulatie van het lichaam. Anders gezegd, bij orale toediening van morfine is de biologische beschikbaarheid van deze stof laag (ongeveer 40%), zeker in vergelijking met een toediening via een intraveneuze bolusinjectie (d.w.z. een inspuiting van de stof in één keer in een bloedader) met een biologische beschikbaarheid van bijna 100%. Onderstaande figuur illustreert een ander voorbeeld: de manier waarop cocaïne gebruikt wordt speelt een grote rol bij het verloop van de concentratie van de stof in het bloedplasma. Bij inspuiting of roken wordt een hoge piekwaarde van de plasmaconcentratie al naar een paar minuten bereikt, terwijl bij een orale toediening pas na een half uur enige stijging in de plasmaconcentratie waar te nemen is en pas na meer dan één uur de piekwaarde bereikt wordt.

In dit voorbeeld gaan we een simpel model voor een oraal toegediend farmacon bestuderen en zien hoe de methode van een integrerende factor een exacte oplossing van het model oplevert.

De orale toediening, dat wil zeggen het slikken van tabletten of het nuttigen van medicinale drank, wordt het meest gebruikt bij toediening van medicijnen. Het medicijn komt dan eerst in de maag terecht. Met enige vertraging komt het farmacon vervolgens in de dunne darm; de vertraging is in een concentratie-tijdkromme te zien doordat de concentratie pas een tijdje \((t_{lag}\)) na orale toediening begint te stijgen. In de wiskundige modelering zullen we deze vertraging negeren door net te doen of alle hoeveelheid op tijdstip \(t=0\) al de dunne darm bereikt heeft en dat daarvandaan absorptie van het farmacon kan plaatsvinden. Vanuit de dunne darm komt het farmacon namelijk d.m.v. een diffusieproces via de poortader in de lever terecht. Het absorptieproces volgt in deze stap voornamelijk eerste-orde kinetiek vanwege passieve diffusie. De lever laat echter maar een beperkt deel onveranderd doorgaan naar de algemene bloedcirculatie van het lichaam (voorbij de poortader en de lever). Via het bloed verspreidt het doorgelaten farmacon zich vervolgens verder over het lichaam en kan zijn therapeutische werking doen.

Zodra het geabsorbeerde farmacon zich verdeeld over het lichaam ondergaat het ook het proces van eliminatie. In het begin overstijgt de geabsorbeerde hoeveelheid de geëlimineerde hoeveelheid met als gevolg dat de plasmaconcentratie stijgt. Op het maximum is de absorptie even groot als de eliminatie. Na verloop van tijd, wanneer het absorptieproces op zijn einde loopt, overheerst de eliminatie; de concentratie neemt dan af in de loop van de tijd. Onderstaande grafiek toont de typische vorm van concentratie-tijdkromme voor een oraal toegediend farmacon.

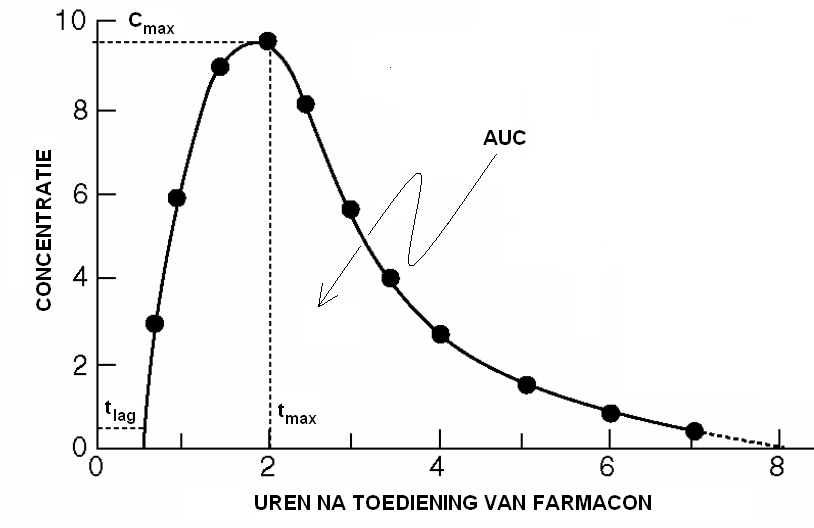
De fractie van het toegediende farmacon dat onveranderd in de algemene bloedcirculatie terechtkomt wordt in de Nederlandse vakliteratuur de biologische beschikbaarheid van het farmacon genoemd. Deze grootheid wordt in formules meestal aangeduid met de hoofdletter \(F\). Daarnaast speelt ook de snelheid van absorptie een rol bij de bepaling van de therapeutische kwaliteit van een geneesmiddel. De Amerikaanse definitie voor ‘bioavailablity’ omvat beide facetten, snelheid en mate van absorptie. Dan duidt de term ‘absolute bioavailablity’ de fractie van de stof die geabsorbeerd wordt aan. Een lage biologische beschikbaarheid van een farmacon kan verschillende oorzaken hebben: slechte wateroplosbaarheid (leidend tot het niet volledig oplossen van een stof), ontleding in het maag-darmkanaal, onvolledig vrijkomen door gebrekkige toedieningsvorm, ‘first-pass metabolisme’ in de lever (d.w.z. biotransformatie na eerste of meerdere passages in de lever) en interacties met andere stoffen (bijvoorbeeld andere farmaca) in het lichaam zijn enkele van de mogelijke redenen. De biologische beschikbaarheid van een farmacon dat gevoelig is voor snelle biotransformatie tijdens de passage van de darmwand en de lever zal laag zijn. Bijvoorbeeld wordt 60-80% van een orale dosis van de bètablokker propranolol tijdens de eerste passage door de lever geblokkeerd. Voor de bepaling van de biologische beschikbaarheid wordt meestal het concentratie-verloop in bloed, serum of plasma in de tijd als uitgangspunt genomen en meer in het bijzonder de oppervlakte onder de concentratie-tijdkromme (AUC, ‘area under the curve’) genomen. De oppervlakte vanaf tijdstip nul tot oneindig is een veelgebruikte maat voor de biologische activiteit. De gebruikte formule voor een open één-compartimentmodel is dan zoals eerder gezien hebben: \[F=\frac{\mathrm{AUC}\cdot \mathrm{Cl}}{D},\] waarbij \(D\) de toegediende dosis is en \(\mathrm{Cl}\) de klaring van het farmacon. Als maat voor de snelheid van opname van een farmacon gelden de piekspiegel \(C_\mathrm{max}\) en de tijdsduur \(C_\mathrm{max}\) waarop deze bereikt wordt.

GDV van plasmaconcentratie van een farmacon bij orale toediening In het vervolg van deze sectie veronderstellen we een open één-compartmentmodel met eerste-orde kinetiek voor zowel de absorptie- als eliminatiefase, met absorptiesnelheidsconstante \(k_a\) en eliminatiesnelheidsconstante \(k\). Er zal blijken dat het verloop van de plasmaconcentratie van een farmacon, onder voorwaarde dat de absorptiesnelheidsconstante groter is dan de eliminatiesnelheidsconstante, wiskundig beschreven wordt door een bi-exponentiële functie, met een term voor absorptie en eliminatie. Onderstaande figuur toont een grafische weergave van het model voor orale toediening van een farmacon met eerste-orde kinetiek voor absorptie in en eliminatie uit het lichaam, beschouwd als één centraal compartiment:

Dit plaatje stelt het volgende voor: uit de dunne darm wordt het farmacon geabsorbeerd en komt via de lever voor een deel in de algemene bloedcirculatie terecht. Voor de afname van het farmacon uit de dunne darm hanteren we een exponentieel model met eliminatiesnelheidsconstante \(k_a\). Dus: \[\frac{\dd A_\mathrm{dunne\;darm}}{\dd t}=-k_a\cdot A_\mathrm{dunne\;darm}\] waarbij \(A_\mathrm{dunne\;darm}\) de hoeveelheid farmacon in de dunne darm is. De snelheid waarmee dit in de algemene bloedcirculatie komt heeft tegengesteld teken en slechts een fractie \(F\) van het farmacon passeert de dunne darm en lever. In formulevorm is de absorptiecomponent van de verandering van hoeveelheid farmacon in de centrale component gelijk aan het volgende: \[\left(\frac{\dd A_\mathrm{centrale\;component}}{\dd t}\right)_\mathrm{absorptie}= F\cdot k_a\cdot A_\mathrm{dunne\;darm}\] De eerste-orde kinetiek van eliminatie kan opgeschreven worden in wiskundetaal als \[\left(\frac{\dd A_\mathrm{centrale\;component}}{\dd t}\right)_\mathrm{eliminatie}= -k\cdot A_\mathrm{centrale\;component}\] Optellen van de formules voor absorptie en eliminatie geeft de formule voor de verandering van het farmacon in de centrale component en, samen met de formule voor eliminatie uit de dunne darm, een tweetal vergelijkingen die de verandering van hoeveelheden farmacon in dunne darm en de centrale component samen beschrijven: \[\begin{aligned} \frac{\dd A_\mathrm{dunne\;darm}}{\dd t} &=-k_a\cdot A_\mathrm{dunne\;darm}\\ \\ \frac{\dd A_\mathrm{centrale\;component}}{\dd t}&=F\cdot k_a\cdot A_\mathrm{dunne\;darm}-k\cdot A_\mathrm{centrale\;component}\end{aligned}\] Deling door het verdelingsvolume \(V_d\) van de centrale component geeft dit stelsel van vergelijkingen in termen van de hoeveelheid farmacon in de dunne darm en de plasmaconcentratie \(C\): \[\begin{aligned} \frac{\dd A_\mathrm{dunne\;darm}}{\dd t} &=-k_a\cdot A_\mathrm{dunne\;darm}\\ \\ \frac{\dd C}{\dd t}&=\frac{F\cdot k_a}{V_d}\cdot A_\mathrm{dunne\;darm}-k\cdot C\\ \end{aligned}\] De eerste vergelijking hoort bij exponentieel verval en heeft als oplossing \[A_\mathrm{dunne\;darm}=A_0\,e^{-k_a\,t}\] waarbij \(A_0\) de beginhoeveelheid van het farmacon in de dunne darm is en dus gelijk aan de toegediende dosis van het farmacon is. Invullen van deze formule in de tweede gelijkheid geeft: \[\frac{\dd C}{\dd t}=\frac{F\cdot k_a\cdot A_0}{V_d}\cdot e^{-k_a\,t}-k\cdot C\] Deze vergelijking is van de volgende vorm: \[\frac{\dd C}{\dd t}=\alpha e^{-k_a\,t}-k\cdot C,\] voor zekere constante \(\alpha=(F\cdot k_a\cdot A_0)/V_d\).

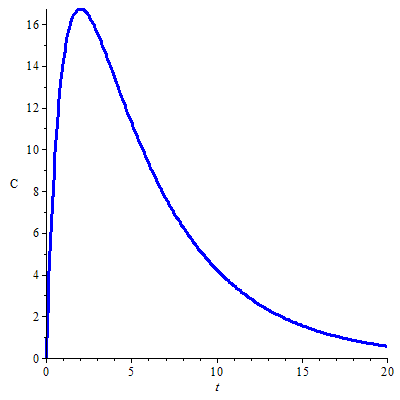
Berekening van het concentratie-tijdprofiel De differentiaalvergelijking \[\frac{\dd C}{\dd t}=\alpha e^{-k_a\,t}-k\cdot C,\] voor zekere constante \(\alpha\), kan m.b.v. een integrerende factor berekend worden. Eerst herschrijven we de vergelijking in differentiaalvorm als \[\dd C+k\,C\,\dd t=\alpha e^{-k_a\,t}\,\dd t\] en vermenigvuldigen met de integrerende factor \(e^{k\,t}\) om te komen tot \[e^{k\,t}\,\dd C+k\,e^{k\,t}\,C\,\dd t=\alpha e^{(k-k_a)t}\,\dd t\] Linker- en rechterlid van de vergelijking zijn differentialen van functies; als \(k\neq k_a\) dan \[\dd\left(e^{k\,t}\,C\right)=\dd\left(\frac{\alpha}{k-k_a}\,e^{(k-k_a)t}\right)\] Hieruit volgt dat \[e^{k\,t}\,C=\frac{\alpha}{k-k_a}\,e^{(k-k_a)t}+\beta\] oftewel \[C=\frac{\alpha}{k-k_a}\,e^{-k_a\,t}+\beta e^{-k\,t}\] voor zekere integratieconstante \(\beta\). Als verondersteld wordt dat \(C(0)=0\), dan geldt dat \(\alpha/(k-k_a)+\beta=0\) oftewel \(\beta=\alpha/(k_a-k)\) en dat de oplossing van de GDV geschreven kan worden als \[C=\frac{\alpha}{k_a-k}\left(e^{-k\,t}- e^{-k_a\,t}\right).\] We hebben dus de volgende algemene formule gevonden voor de plasmaconcentratie \(C\) onder de voorwaarde dat \(k\neq k_a\): \[C=\frac{k_a A_0 F }{V_d{(k_a-k)}}\left(e^{-k\,t}- e^{-k_a\,t}\right)\] Dit is een bi-exponentiële functie. Onderstaande figuur toont de grafiek van de plasmaconcentratie van een farmacon berekend met de volgende farmacokinetische parameters: \[\text{orale dosis }A_0=500\,\mathrm{mg},\; k_a=1.0\,\mathrm{h}^{-1},\; k=0.2\,\mathrm{h}^{-1}, \;V_d=10\,\mathrm{L}, F=0.5\]