We consider the example of a mechanical vibration of a suspended mass-spring system. Suppose that a ball (mass $m$ kg) is suspended by a spring of negligible mass. Suppose the $x$ axis is vertical (we will explain why later), with the positive direction downwards and the origin the equilibrium position of the ball (because of this choice we can keep gravity outside of the equations). See the diagram below.

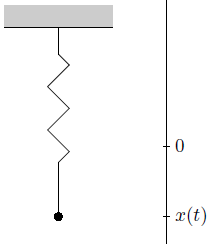If the ball is moved away from the equilibrium position and then released from rest, it will perform a vibration: it will move up and down. According to Hooke's law, the force of the spring acting on the ball is proportional to the deflection $x$ and directed in opposite direction, hence of the form $-k\,x$, where $k$ is a positive constant, referred to as the spring constant. We assume for convenience that there is no resistance. According to Newton's second law: $$m\, x''(t)=-k\, x(t)\, , \; x(0)=x_0\, ,\; x'(0)=0,$$ where $x_0$ is the initial deflection of the ball; $x'(0)=0$ indicates that the ball was at rest at time 0. We have a homogeneous linear differential equation with constant coefficients of order 2, and the characteristic equation $$m\lambda^2+k =0$$ has two complex solution, namely $\lambda_{1,2}=\pm \sqrt{\dfrac{k}{m}}$. It follows that: $$x(t)=A\,\cos\left(\sqrt{k\over m}\,t\right) +B\,\sin\left(\sqrt{k\over m}\, t\right)$$ The initial conditions lead to $$x(t)=x_0\cos\left(\sqrt{k\over m}\, t\right)$$ The ball carries out a so-called harmonic vibration.

It is realistic to take into account the influence of air resistance: we suppose this force is proportional to the speed of the ball and in opposite direction, this results in the equation: $$m\, x''(t)+\mu\, x'(t) +k\, x(t)=0$$ with the same initial conditions as before: $x(0)$ and $x'(0)$. Here, $\mu$ is a positive constant that describes the frictional force due to air resistance. It depends on the discriminant of the characteristic polynomial $m\lambda^2+\mu\lambda +k$ what the solution looks like exactly.

For example, if $m=1, \mu=2, k=2$, then the characteristic equation is $(\lambda+1)^2+1=0$ with solutions $\lambda_{1,2}=-1\pm\mathrm{i}$, and the deflection is given by $x(t)$ as $$x(t)=A\,e^{-t}\cos t+B\,e^{-t}\sin t$$ The values of $A$ and $B$ follow from the initial conditions, but from the shape of the mathematical formula you can already see that this concerns a damped oscillation in which the spring eventually returns to the equilibrium position.

By adding an inhomogeneous term, say $f(t)$, to the homogeneous differential equation you get the mathematical model of a forced vibration: $$m\, x''(t)+\mu\, x'(t) +k\, x=f(t)$$ It can be shown that the general solution of this differential equation is equal to the sum of the general solution of the corresponding homogeneous differential equation and one specific solution of the differential equation. But we will not discuss that ihere.

We return to the choice of the letter $x$ for vertical deflection. We did this to make an easier transition from the mathematical model above to a model of coupled non-linear differential equations. For this we introduce the function $y(t)$ as the derivative $x(t)$. Then we can rewrite the original differential equation $$m\, x''(t)+\mu\, x'(t) +k\, x(t)=0$$ as $$m\, y'(t)+\mu\, y(t)+k \,x(t)=0$$ This leads to the following system of linear differential equations $$\left\{\begin{aligned} x'(t) &= y(t)\\ y'(t) &= -\frac{\mu}{m}y(t)-\frac{k}{m} x(t)\end{aligned}\right.$$

So we have a special case of a linear system of coupled first order differential equations that can be written in the form: $$\left\{\begin{aligned} x'(t) &= a\, x(t)+ b\, y(t)\\ y'(t) &= c\, x(t) + d\, y(t)\end{aligned}\right.$$