We bekijken het voorbeeld van een mechanische trilling van een opgehangen massa-veersysteem. Stel dat een massapunt (\(m\) kg) aan een veer van verwaarloosbare massa hangt. We leggen de \(x\)-as verticaal (later wordt duidelijk waarom), met de positieve richting naar beneden en de oorsprong in de evenwichtstand van het bolletje (door deze keuze kunnen we de zwaartekracht buiten de discussie houden). Zie onderstaande schets.

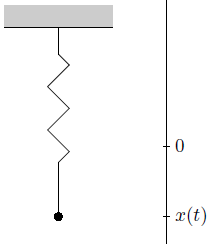Als het bolletje uit de evenwichtstand gehaald is en uit rust losgelaten wordt, gaat het een trilling uitvoeren. De veerkracht werkend op het bolletje is volgens de wet van Hooke evenredig met de uitwijking \(x\) en tegengesteld daaraan gericht, dus van de vorm \(-k\,x\), waarin \(k\) een positieve constante is, de veerconstante genoemd. We veronderstellen gemakshalve dat het bolletje geen luchtweerstand ondervindt. Er geldt dan volgens de Tweede Wet van Newton: \[m\, x''(t)=-k\, x(t)\, , \; x(0)=x_0\, ,\; x'(0)=0\] Hierin is \(x_0\) de beginuitwijking van het massapunt; \(x'(0)=0\) geeft aan dat het punt op tijdstip 0 in rust is. We hebben een homogene lineaire differentiaalvergelijking van orde 2 met constante coëfficiënten en de karakteristieke vergelijking \[m\lambda^2+k =0\] heeft twee complexe oplossing, namelijk \(\lambda_{1,2}=\pm \sqrt{\dfrac{k}{m}}\). Er volgt dat: \[x(t)=A\,\cos\left(\sqrt{k\over m}\,t\right) +B\,\sin\left(\sqrt{k\over m}\, t\right)\] De beginvoorwaarden leiden tot \[x(t)=x_0\cos\left(\sqrt{k\over m}\, t\right)\] Het bolletje voert een zogenaamde harmonische trilling uit.

Het is realistischer ook rekening te houden met de invloed van de luchtweerstand: deze kracht veronderstellen we evenredig met de snelheid van het bolletje en tegengesteld gericht daaraan Dit leidt tot de vergelijking: \[m\,x''(t)+\mu\, x'(t) +k\, x(t)=0\] met voorgeschreven beginvoorwaarden \(x(0)\) en \(x'(0)\). Hierin is \(\mu\) een positieve constante die voor de wrijvingskracht ten gevolge van de luchtweerstand verantwoordelijk is. Het hangt van de discriminant van de karakteristieke veelterm \(m\lambda^2+\mu\lambda +k\) af hoe de oplossing er precies uitziet.

Bijvoorbeeld, als \(m=1, \mu=2, k=2\), dan is de karakteristieke vergelijking \((\lambda+1)^2+1=0\), met oplossingen \(\lambda_{1,2}=-1\pm\mathrm{i}\), en heeft de uitwijking \(x(t)\) de vorm \[x(t)=A\,e^{-t}\cos t+B\,e^{-t}\sin t\] De waarden van \(A\) en \(B\) hierin volgen uit de beginvoorwaarden, maar aan de vorm van de wiskundige formule kun je al wel zien dat het hier gaat om een gedempte trilling waarbij de veer uiteindelijk terugkeert naar de evenwichtstand.

Door aan de homogene differentiaalvergelijking een inhomogene term, zeg \(f(t)\), toe te voegen krijg je het wiskundige model van een gedwongen trilling: \[m\, x''(t)+\mu\, x'(t) +k\, x(t)=f(t)\] Bewezen kan worden dat de algemene oplossing van deze differentiaalvergelijking gelijk is aan de som van de algemene oplossing van de bijpassende homogene differentiaalvergelijking en één specifieke oplossing van de differentiaalvergelijking. Maar we gaan hier in deze wiskunde module niet verder op in.

Keren we nog terug op de keuze van de letter \(x\) voor de verticale uitwijking. Dit hebben we gedaan om een gemakkelijkere overgang te maken van bovenstaand wiskundig model naar een model van gekoppelde lineaire differentiaalvergelijkingen. Hiervoor introduceren we de functie \(y(t)\) als afgeleide van \(x(t)\). Dan kunnen we de oorspronkelijke differentiaalvergelijking \[m x''(t)+\mu x'(t) +k \,x(t)=0\] herschrijven als\[m\,y'(t)+\mu\, y(t)+k \,x(t)=0\] Dit leidt tot het volgende stelsel van lineaire differentiaalvergelijkingen \[\left\{\begin{aligned} x'(t) &= y(t)\\ y'(t) &= -\frac{\mu}{m}y(t)-\frac{k}{m} x(t)\end{aligned}\right.\]

We hebben hier dus te maken met een speciaal geval van het volgende stelsel van gekoppelde lineaire eerste-orde differentiaalvergelijkingen, dat op te schrijven is de volgende vorm: \[\left\{\begin{aligned} x'(t) &= a\, x(t)+ b\, y(t)\\ y'(t) &= c\, x(t) + d\, y(t)\end{aligned}\right.\]