Gewone differentiaalvergelijkingen: Lineaire tweede-orde GDVs met constante coëfficiënten
 Stelsels van gekoppelde lineaire eerste-orde GDVs
Stelsels van gekoppelde lineaire eerste-orde GDVs
Van een 2-dimensionaal stelsel van homogene eerste-orde lineaire GDVs naar een homogene tweede-orde lineaire GDV We bekijken het volgende stelsel van gekoppelde homogene eerste-orde lineaire differentiaalvergelijkingen: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= a\, x+ b\, y\\[0.25cm] \frac{\dd y}{\dd t} &= c\, x + d\, y\end{aligned}\right.\] We kunnen dit stelsel ook omwerken tot een homogene tweede-orde lineaire differentiaalvergelijking met constante coëfficiënten voor \(x(t)\) en een soortgelijke differentiaalvergelijking voor \(y(t)\). Dit betekent dat we het stelsel kunnen oplossen!
Het vinden van de bijpassende GDV Laten we eens nagaan hoe dit in zijn werk gaat voor \(x(t)\). Differentiëren we linker- en rechterkant van de eerste vergelijking in het stelsel, dan krijgen we \[\frac{\dd^2x}{\dd t^2}=a\frac{\dd x}{\dd t}+b\frac{\dd y}{\dd t}\] en na substitutie van de tweede vergelijking van het stelsel \[\frac{\dd^2x}{\dd t^2}=a\frac{\dd x}{\dd t}+b\,c\,x + b\,d\,y\] De eerste vergelijking van het stelsel kunnen we ook opschrijven als \(b\,y =\frac{\dd x}{\dd t}-a\, x\) en substitutie leidt dan tot de gewenste tweede-orde GDV, die opgeschreven kan worden als:\[ \frac{\dd^2x}{\dd t^2}-(a+d)\frac{\dd x}{\dd t}+(ad-bc)x =0\]
Oplossen van het stelsel We weten hoe we bovenstaande twee-orde GDV kunnen oplossen en dat het gedrag afhangt van de discriminant van de bijpassende karakteristieke veelterm \[\lambda^2 -(a+d)\lambda+(ad-bc)\] Deze discriminant \(D\) kunnen we herschrijven: \[D=(a+d)^2-4(ad-bc)=(a-d)^2+4bc\] We hebben nu drie gevallen te onderscheiden:
- Als \((a-d)^2+4bc>0\) dan zijn er twee reële wortels van de karakteristieke veelterm: \[\lambda_{1,2}=\frac{a+d\pm\sqrt{(a-d)^2+4bc}}{2}\] en de algemene oplossing voor \(x(t)\) is dan \[x(t)=c_1e^{\lambda_1t}+c_1e^{\lambda_2t}\]
- Als \((a-d)^2+4bc=0\) dan is er één reële wortel van de karakteristieke veelterm: \[\lambda=\frac{a+d}{2}\] en de algemene oplossing voor \(x(t)\) is dan \[x(t)=(c_1+c_2 t)e^{\lambda t}\]
- Als \((a-d)^2+4bc<0\) dan zijn er twee imaginaire wortels van de karakteristieke veelterm: \[\lambda_{1,2}=\alpha\pm\mathrm{i}\,\beta\] met \[\alpha=\frac{a+d}{2}\quad\text{en}\quad\beta=\frac{\sqrt{-(a-d)^2-4bc}}{2}\] en de algemene oplossing voor \(x(t)\) is dan \[x(t)=e^{\alpha t}\bigl(c_1\cos(\beta t)+c_2\sin(\beta t)\bigr)\]
\(\phantom{abc}\)
Voor \(y\) kun je op soortgelijke wijze te werk gaan.
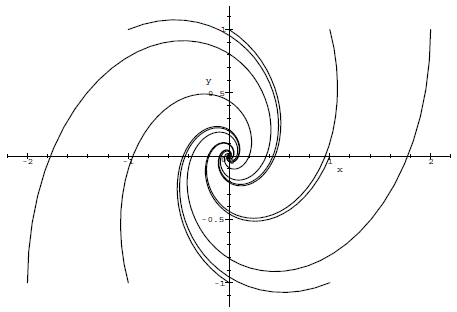
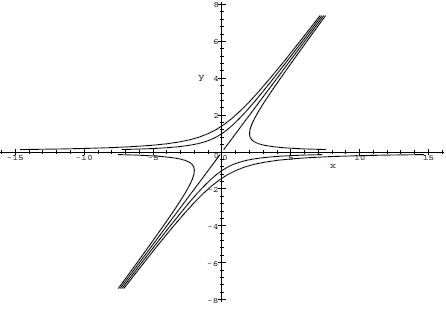
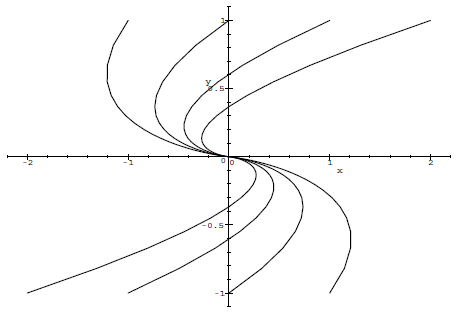
Oplossingskrommen bij een 2-dimensionaal stelsel van 1ste-orde lineaire GDVs Om een beter inzicht te krijgen in het gedrag van de oplossingen van het stelsel van gekoppelde homogene eerste-orde lineaire differentiaalvergelijkingen gebruikt men meestal het zogenaamde faseportret of faseplaatje. Je tekent dan parameterkrommen \( t\mapsto (x(t), y(t))\) voor verschillende beginvoorwaarden van de differentiaalvergelijking (en eventueel een zogenaamd richtingsveld als achtergrond, hetgeen we hier weglaten): de oplossingen \(x(t)\) en \(y(t)\) zijn dus coördinaatfuncties van een kromme in het platte vlak. De oplossingskrommen geven een goede indruk van het gedrag van beide oplossingen samen. Zonder bewijs, tonen we enkele plaatjes van verschillende soorten faseportretten die op kunnen optreden (het zijn geen uitputtende voorbeelden en we laten ook niet zien in welke richting de krommen gaan).
- een negatieve en een positieve reële wortel van de karakteristieke veelterm:
- één reële wortel van de karakteristieke veelterm:
- twee complexe wortels van de karakteristieke veelterm: