The name forward Euler method suggests that there is also a backward Euler method for the numerical solution of first-order ODEs exists. This is correct, but the numerous algorithms for the numerically solving differential equations are beyond the scope of this instuctional unit. The most important message is only that such numerical solution methods do exist and can be made use of.

Note that if you use in the forward Euler method a negative time step \(dt\), preceding values in an integral curve are calculated . So the Euler method is suitable for computing integral curves through a certain point toward past and future. In the figure below, the integral curves of the ODE \[\frac{\dd y}{\dd t}=3e^{-t}-y,\] through the points \((2,0),\;(1,1),\;(0,2)\) have been plotted.

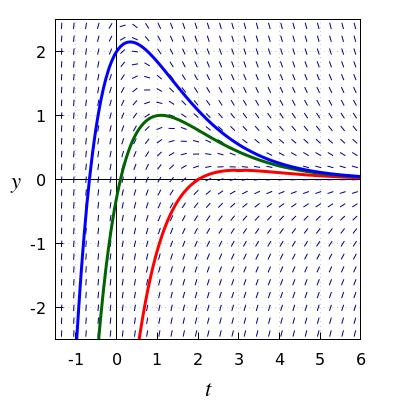
This may seem to be a contrived example, but the green integral curve does have the conventional shape of the concentration profile of an orally administered drug whose pharmacokinetics can be described with an open central compartment and with first-order kinetics for the absorption and elimination according to an exponential model.