Ordinary differential equations: Asymptotics and stability
 Stability
Stability
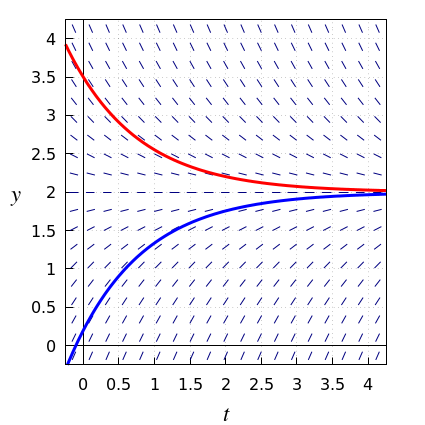
Frequent behaviour of a solution of a differential equation is that it approaches a constant value in the course of time and that the constant value itself is a particular solution, namely an equilibrium. We already had a short look at the behaviour of sigmoidal solutions of the logistic differential equation. Let us now explore the following differential equation of limited exponential growth: \[\frac{\dd y}{\dd t}=2-y\] In the slope field two solution curves are shown and they illustrate that a solution of this differential equation always approaches \(y=2\) for large values of \(t\). \(y(t)=2\) itself is a solution of the differential equation; it is called the equilibrium solution (shortly, equilibrium), fixed point solution, or steady state.
The general case of limited exponential growth is not difficult either. Consider the differential equation \[\frac{\dd y}{\dd t}=r\cdot (a-y)\] for positive constants \(r\) and \(a\). There exists an equilibrium and we can find it by solving the equation \(\frac{\dd y}{\dd t}=0\). The solution of the linear equation \(r\cdot (a-y)=0\) is easy to find and is \(y=a\).
Of course you can also release the requirements of positivity of \(r\) and \(a\).
Stability and asymptotics of limited exponential growth Consider the differential equation \[\frac{\dd y}{\dd t}=r\cdot (a-y)\] for constants \(r\neq 0\) and \(a\). The solution \[y=a\] is an equilibrium.
If \(r>0\), then any solution of the differential equation always approaches \(y=a\) for large values of \(t\). In other words, we have attracting equilibrium. We also refer to this as a stable equilibrium or attractor.
If \(r<0\), then any solution of the differential equation different from the equilibrium increasingly moves away from \(y=a\) for large values of \(t\). In other words, we have a repelling equilibrium. We also refer to this as an unstable equilibrium or repeller.
Example of a semi-stable equilibrium Besides a stable or unstable equilibrium, often referred to as the non-hyperbolic equilibria, there is a third option, namely, a semi-stable equilibrium, also referred to as a half-stable equilibrium. In this case, the behaviour of a solution depends on where the solution is located with respect to the equilibrium. The previously discussed ODE with the blow-up phenomenon \[\frac{\dd y}{\dd t}=y^2\] illustrates this.
There is an equilibrium \(y=0\). The general solution is a rational function of the form \[y(t)=\frac{1}{c-t}\] for some constant \(c\). But in fact, this formula describes two solutions: for \(t<c\) we have a solution that runs away from the equilibrium over time and for \(t>c\) we have a solution that approaches the equilibrium as time passes. In other words: a solution curve with positive function values moves away from the equilibrium in the course of time and a solution curve with negative function values approaches the equilibrium in the course of time. The equilibrium is from one side a repeller and from the other side an attractor.


